Kumpulan Soal Latihan Lengkap Bangun Datar

Hello teman-teman kembali lagi kita pada materi tentang Kumpulan Soal Latihan Lengkap Bangun Datar. sebelumnya kita sudah membahas tentang luas arsiran pada bangun datar. bangun datar terbagi atas delapan bagian yaitu: persegi, persegi panjang, belah ketupat, layang-layang, jajar genjang, trapesium, segitiga, dan lingkaran. bangun datar adalah suatu bidang yang dibatasi oleh garis-garis lurus atau garis-garis lengkung pada bangun datar.

Daftar Isi

1. Macam-Macam Bangun Datar
2. Kumpulan Materi Soal Latihan Lengkap Bangun Datar
3. Soal Latihan Lengkap Bangun Datar
4. Saran dan Kritik Tentang  Soal Latihan Lengkap Bangun Datar 

Macam-Macam Bangun Datar

beberapa kumpulan rumus bangun datar:

» Bangun Datar Persegi

persegi adalah jumlah panjang keempat sisiya yang saling kongruen. 

Panjang = sisi

Lebar = Sisi

Sisi sering disimbolkan s

Keliling Persegi Panjang = S + S + S + S

Keliling Persegi Panjang = 4S

Luas Persegi = s x s

» Bangun Datar Persegi Panjang

persegi panjang adalah Bangun Datar segiempat yang keempat sudutnya siku-siku dan sisi-sisi yang berhadapan sama panjang dan sejajar.

Keterangan:

P = panjang

L = lebar

Keliling Persegi Panjang = P + P + L + L

Keliling Persegi Panjang = 2P + 2L

Keliling Persegi Panjang = 2(P + L)

Luas Persegi Panjang = p x l

» Bangun Datar Belah ketupat

Belah ketupat adalah Bangun Datar segiempat dengan sisi yang berhadapan sejajar, keempat sisinya kongruen atau sama panjang, dan sudut-sudut yang berhadapan sama besar. 

keterangan:

s = sisi

keliling belahketupat = 4s

D1 = diagonal pertama

D2 = diagonal kedua

Maka rumus luas belah ketupat:

Luas Belahketupat = ½ diagonal x diagonal lainnya

» Bangun Datar Layang-Layang

Layang-layang adalah Bangun Datar segiempat yang masing-masing pasang sisinya sama panjang dan sudut yang saling berhadapan kongruen atau sama besar. 

keliling layang-layang = jumlah keseluruhan sisinya

keterangan:

D1 = diagonal pertama

D2 = diagonal kedua

Maka rumus luas belah ketupat:

Luas Layang-Layang = ½ diagonal x diagonal lainnya

» Bangun Datar Trapesium

trapesium adalah Bangun Datar segi empat dengan tepat sepasang sisi yang berhadapan sejajar.

keliling layang-layang = jumlah keseluruhan sisinya

Luas Trapesium = ½ (jumlah sisi sejajar) x tinggi

» Bangun Datar Segitiga

Segitiga adalah suatu bangun datar yang memiliki tiga sisi dan jumlah keseluruhan sudutnya 180 derajat

Keliling Segitiga = jumlah ketiga sisinya.

Luas Segitiga = ½ (alas x tinggi)

» Bangun Jajar Genjang

Jajargenjang adalah Bangun Datar segiempat dengan sisi-sisi yang berhadapan sejajar dan sama panjang serta sudut-sudut yang berhadapan sama besar.

keliling layang-layang = jumlah keseluruhan sisinya

Luas Jajar genjang = alas x tinggi

» Bangun Datar Lingkaran

Lingkaran adalah kumpulan titik-titik yang membentuk sebuah garis yang melengkung apabila dihubungkan dengan pusatnya akan memiliki jarak yang sama.

Keliling lingkaran = 2πr

Luas Lingkaran = π$r^{2}$ 

Kumpulan Materi Soal Latihan Lengkap Bangun Datar

Kumpulan Materi Bangun Datar: 40

1. Bank Soal Tentang Sudut Matematika
2. Bank Soal Latihan Lengkap Hubungan Sudut dan Garis
3. Menentukan Sudut antara Dua Tali Busur Lingkaran
4. Segi Empat Tali Busur dalam Lingkaran Serta Sifat-Sifatnya
5. Menentukan Panjang Jari-Jari, Diameter, Tali Busur, Juring, Apotema, Busur, Tembereng, Luas & Keliling Lingkaran
6. Kumpulan Latihan Soal Lengkap Lingkaran
7. Rumus Bangun Datar Lengkap
8. Bagiamana Cara Menentukan Hubungan Besar Sudut dan Panjang Sisi Suatu Segitiga
9. Menemukan Nilai Pi (π) Lingkaran
10. Menghitung Tinggi, Panjang Salah Satu Sisi yang tidak Diketahui, Keliling, dan Luas pada Segitiga Sama Kaki
11. Menghitung Tinggi, Panjang Salah Satu Sisi yang tidak Diketahui, Keliling, dan Luas pada Segitiga Sama Sisi
12. Menghitung Tinggi, Keliling, dan Luas pada Segitiga Sembarang
13. Cara Menentukan Luas Daerah Arsir pada Bangun Datar
14. Bagaimana Cara Menentukan Garis Bagi pada Segitiga
15. Bagaimana Cara Menentukan Perbandingan Segmen Garis Pada Segitiga
16. Bagaimana Cara Menentukan Titik Berat pada Segitiga
17. Menentukan Besar Sudut pada Segitiga Siku-Siku Menggunakan Aturan Trigonometri
18. Cara Menentukan Besar Sudut Segitiga Sembarang Menggunakan Rumus Cosinus
19. Contoh Penerapan Teorema Pythagoras atau Segitiga Siku-siku Dalam Kehidupan Sehari-hari
20. Cara Menentukan Panjang Sisi Segitiga dengan Menggunakan Rumus Sinus
21. Penerapan Trigonometri pada Segitiga dan Fungsinya Dalam Kehidupan Sehari-hari
22. Kumpulan Soal Latihan Lengkap pada Segitiga
23. Latihan Soal Lengkap Pertama Lingkaran
24. Kumpulan Soal Latihan Lengkap Bangun Datar
25. Bagaimana Cara Menentukan panjang garis berat pada segitiga
26. Hubungan Sudut Luar dan Dalam Segitiga
27. Bagaimana Cara Menentukan Panjang Tali Busur Lingkaran
28. Garis Singgung Melalui Titik di Luar Lingkaran
29. Lingkaran Dalam Pada Segitiga Sembarang
30. Lingkaran Dalam Segitiga Sama Sisi
31. Menghitung Luas, Keliling , serta Panjang Jari-Jari Lingkaran dalam Segitiga Siku-Siku
32. Menentukan Titik Potong Tali Busur di Luar Lingkaran
33. Macam-macam Bangun Datar, Serta Rumus dan Sifatnya
34. Tips Mudah Belajar Kesebangunan Dan Kekongruenan: (Pengertian, Sifat-Sifat, dan Pembahasan Soal)
35. Bagaimana Cara Menentukan Hubungan Sudut Pada Dua Garis Sejajar
36. Bagaimana Cara Menentukan Keliling dan Luas Segitiga
37. Tips Belajar Mudah Trapesium: (Pengertian, Sifat-Sifat, Keliling, Luas, Pembahasan Soal)
38. Belah Ketupat : (Pengertian, Sifat-Sifat, Keliling, Luas, dan Pembahasan Soal)
39. Trik Mudah Belajar Jajar Genjang: (Pengertian, Sifat-Sifat, Keliling & Luas, Pembahasan Soal)
40. Trik Cepat Belajar Layang-Layang : (Pengertian, Sifat-Sifat, Keliling & Luas, Pembahasan Soal)

Soal Latihan Lengkap Bangun Datar

Contoh Soal 1

Perhatikan gambar dibawah ini:

Hitunglah keliling persegi yang panjang sisinya 12 cm

Penyelesaian:

Sisi = 12 cm

Keliling persegi = 12s

Keliling persegi = 12 x 4

Keliling persegi = 48 cm

contoh soal 2

Keliling persegi panjang = 100 cm. jika panjangnya lebih 10 cm dari lebarnya, hitunglah panjang dan lebarnya……..?

Penyelesaian:

Lebar = x cm

Panjang = (x + 10) cm

Keliling persegi panjang = 100 cm,

Keliling Persegi Panjang = 2(P + L)

Keliling Persegi Panjang = 2(x + (x + 10))

100 = 2(2x + 10)

50 = 2x + 10

2x + 10 = 50

2x = 50 – 10

2x = 40   ……………kedua ruas dibagi 2

x = 20

Lebar = 20 cm

Panjang = (x + 10) cm

Panjang = (20 + 10) cm = 30 cm

contoh soal 3

Perhatikan gambar dibawah ini:

Hitunglah luas layang-layangnya:

d₁ = 44 m

d₂ = 22 m

Luas Layang-Layang = ½ (d₁ x d₂)

Luas Layang-layang = ½ (44 x 22)

Luas Layang-layang = 22 x 22

Luas layang-layang = 484 m²

contoh soal 4

Perhatikan gambar dibawah ini:

Tentukanlah keliling jajargenjang….?

Penyelesaian:

Untuk menentukan keliling jajargenjang tentukanlah dulu keseluruhan panjang sisinya

Untuk menentukan panjang BC kita menggunakan teorema Pythagoras dari segitiga BEC. Sisi yang paling terpanjang pada segitiga BEC adalah panjang BC. Maka:

BC² = BE² + EC²

BC² = 3² + 4²

BC² = 9 + 16

BC² = 25

BC = √25

BC = 5 cm

Setelah ditentukan panjang BC barulah kemudian kita cari keliling Jajargenjang:

Panjang BC = 5 cm

Panjang AD = Panjang BC = 5 cm

Panjang AB = 7 cm

Panjang DC = Panjang AB = 7 cm

Sehingga:

Keliling jajargenjang = Jumlah keseluruhan panjang sisinya

Keliling jajargenjang = Panjang BC + Panjang AD + Panjang AB + Panjang DC

Keliling jajargenjang = 5 cm + 5 cm + 7 cm + 7 cm

Keliling jajargenjang = 24 cm

contoh soal 5

Diagonal-diagonal belahketupat PQRS berpotongan di O. salah satu diagonal memiliki panjang 14  cm dan kelilingnya = 100 cm. tentukan panjang diagonal lainnya……?

Penyelesaian:

Keliling belah ketupat = 4s

200 = 4s

4s = 100

s = 25 cm

Tentukan salah satu sisi pada belahketupat menggunakan teorema Pythagoras.

PS² = OP² + OS²

OS = ½ (d₁)

OS = ½ (14 cm) = 7 cm

PS = 25 cm

PS² = OP² + OS²

25² = OP² + 7²

625 = OP² + 49

OP² + 49 = 625

OP² = 576

OP = √576

OP = 24,

Maka panjang diagonal lainnya ……?

d₂ = 24 x 2 = 48 cm

contoh soal 6

Perhatikan gambar dibawah ini:

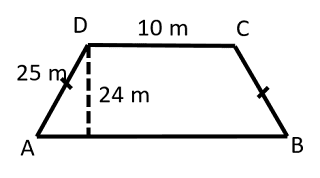
Tentukanlah luas trapezium…..?

Penyelesaian:

Tentukanlah panjang AE, menggunakan rumus teorema Pythagoras:

AE² = AD² – DE²

AD = 25

DE = 24

AE² = 25² – 24²

AE² = 625 – 576

AE² = 49

AE = √49

AE = 7

Luas Trapesium = ½ (jumlah sisi sejajar) x tinggi

Panjang AB = 2.AE + DC

Panjang AB = 2x7 + 10

Panjang AB = 24

Panjang DC = 10 m

Tinggi = 24

Luas Trapesium = ½ (24 + 10) x 24

Luas Trapesium = (34) x 12

Luas Trapesium = 408 m²

contoh soal 7

perhatikan gambar dibawah ini:

tentukanlah luas segitiga diatas................?

penyelesaian:

Luas segitiga = ½ (alas x tinggi)

Alas = 4 cm

Tinggi = 3 cm

Luas segitiga = ½ (4 x 3)

Luas segitiga = 2 x 3

Luas segitiga = 6 cm²

contoh soal 8

perhatikan gambar dibawah ini: tentukanlah luas lingkaran pada gambar diatas........?
r = 28 maka kita menggunakan nilai  π = 22/7 sehingga: luas lingkaran = πr2 luas lingkaran = ($\frac{22}{7}$) (282) luas lingkaran = ($\frac{22}{7}$) (28)(28) luas lingkaran = (22) (4)(28) luas lingkaran = 2.464 cm2

contoh soal 9

pada gambar dibawah ini: Diketahui diameter lingkaran 200 cm, Tentukanlah luas juring lingkaran …..?
a. 208 cm2 b. 408 cm2 c. 308  cm2	d. 108 cm2 e. 306 cm2
Kunci Jawaban: c. x = 1800 d = 200 r = $\frac{1}{2}$ x 200 = 100 cm π = 3,14 Luas Juring Lingkaran = ……? Luas Juring Lingkaran = ($\frac{x}{360}$) x πr2 Luas Juring Lingkaran = ($\frac{180}{360}$) x  (3,14)(100)2 Luas Juring Lingkaran = ($\frac{1}{2}$) (3,14) (100*100) Luas Juring Lingkaran = ($\frac{1}{2}$)  (314) (100) Luas Juring Lingkaran = 314 x 50 Luas Juring Lingkaran = 15.700 cm2

contoh soal 10

pada gambar dibawah ini: Diameter lingkaran diatas 98 cm, Tentukan keliling lingkaran………….?
a. 308 cm b. 208 cm c. 210 cm	d. 2.108 cm e. 2.158 cm
Kunci Jawaban: c. d = 98 r = $\frac{22}{7}$ 98 = 49 π = $\frac{22}{7}$ Keliling Lingkaran = ……? Keliling Lingkaran = 2πr Keliling Lingkaran = 2($\frac{22}{7}$)(49) Keliling Lingkaran =  2 x 22 x 7

contoh soal 11

perhatikan gambar dibawah ini:

diketahui jari-jari lingkaran besar = 15 cm, panjang PQ = 65 cm, dan panjang garis singgung persekutuan dalam lingkaran = 60 cm. tentukanlah jari-jari lingkaran q!

jawaban:

Langkah-langkah menentukan jari-jari lingkarna kecil:

Diketahui: R = 15 cm r = ………. cm jarak titik pusat kedua lingkaran (panjang PQ) disimbolkan JT. JT = 65 cm GSD = 60 cm Sehingga GSD………..? GSD2 = JT2 – (R + r)2 602 = 652 – (15 + r)2 3600 =4225 – (15 + r)2 (15 + r)2 =4225 – 3600 (15 + r)2 = 625 (15 + r) = √625 15 + r = 25 r =25 – 15 r = 10

contoh soal 12

perhatikan gambar dibawah ini:

Diketahui: Panjang garis singgung luar dua lingkaran = 48 cm,panjang AB = 52 cm. dan jari-jari B = 12 cm. tentukanlah jari-jari lingkaran A..?

penyelesaian:

Penyelesaian:

Diketahui: R = …. cm r = 12 cm jarak titik pusat kedua lingkaran (panjang AB) disimbolkan JT. JT = 52 cm GSL = 48 cm Sehingga GSL………..? GSL2 = JT2 – (R - r)2 482 = 522 – (R - 12)2 2304 = 2704 – (R – 12)2 (R – 12)2 =2704 – 2304 (R – 12)2 = 400 (R – 12) = √400 R – 12 = 20 R = 20 + 12 R = 32 R = 32

contoh soal 13

Perhatikan gambar dibawah ini:

Jika Sudut ∆ AOB = 150⁰ tentukanlah berapa sudut ∆ACB ……..?

Penyelesaian:

Sudut pusat lingkaran = ∆ACB

Sudut pusat lingkaran = 150⁰

Sudut Keliling Lingkaran = ½ Sudut Pusat Lingkaran

Sudut Keliling Lingkaran = ½ (150)

Sudut Keliling Lingkaran = 75⁰

Jadi, sudut ∆ACB = 75⁰.

contoh soal 14

perhatikan gambar dibawah ini:

tentukanlah nilai x ...................?

penyelesaian:

Rumus Tripel Pythagoras:

sisi tegak = 21

alasnya = x

Hipotenusa atau sisi terpanjang = 29

Rumus teorema Pythagoras:

21² + x² = 29²

441 + x² = 841

x² = 841 - 441

x² = 400

x = √400

x = 20

contoh soal 15

Perhatikan gambar dibawah ini:

Garis A // B dipotong oleh garis lain. Jika sudut x₁ = 65⁰. Hitunglah besar sudut sudut x₂

 $\angle$x₁ + $\angle$x₂ = 180⁰

65⁰ +  $\angle$x₂ = 180⁰

 $\angle$x₂ = 180⁰ - 65⁰

 $\angle$x₂ = 115⁰

contoh soal 16

Jari-jari lingkaran pada gambar diatas adalah 10 cm. besar sudut ∆AOB = 900.  Tentukanlah tali busur lingkaran ………….?
Kunci Jawaban: c. x = 900 r = 10 cm OA = AB = jari-jari lingkaran, sehingga: OA = 10 OB = 10 Menggunakan rumus teorema Pythagoras. AB = tali busur lingkaran AB2 = OA2 + OB2 – 2 (OA) (OB) cos x AB2 = 102 + 102 – 2 (10) (10) cos 60 AB2 = 100 + 100 – 2 (10) (10) (0) AB2 = 100 + 100 – 0 AB2 = 200 AB = √200 AB = 10√2

contoh soal 17

perhaatikan gambar dibawah ini.

tentukanlah jari-jari lingkaran dalam segitiga siku-siku...........?

penyelesaian:

tahap I tentukanlah luas segitiga siku-siku

Luas Segitiga siku-siku = $\frac{1}{2}$ alas x tinggi

alas segitiga siku-siku = panjang AB = 24 cm

tinggi segitiga siku-siku = Panjang AC = 7 cm

Luas Segitiga siku-siku = $\frac{1}{2}$ x 24 x 7

Luas Segitiga Siku-Siku = 12 x 7

Luas Segitiga Siku-Siku = 84 $cm^{2}$

tahap II tentukanlah keliling segitiga siku-siku

K = AB + AC + BC

AB = 24 cm

AC = 7 cm

BC = ...........? untuk menentukan panjang BC menggunakan rumus teorema pythagoras...?

$BC^{2}$ = $AC^{2}$ + $AB^{2}$

$BC^{2}$ = $24^{2}$ + $7^{2}$

$BC^{2}$ = 576 + 49

$BC^{2}$ = 625

BC = $\sqrt{625}$

BC = 25

K = 25 + 24 + 7

K = 56

tahap III tentukan nilai S

S = $\frac{56}{2}$ = 28 cm

tahap IV tentukan jari-jari lingkaran

keterangan

L = 84 $cm^{2}$

S = 28 cm

r = $\frac{L}{S}$ 

r = $\frac{84}{28}$ 

r = 3 cm

jadi, panjang jari-jari lingkaran dalam segitiga = 3 cm

contoh soal 18

perhatikan gambar dibawah ini:

diketahui panjang sisi segitiga sama = 6 cm. tentukanlah luas lingkaran dalam segitiga sama sisi............?

Langkah Pertama adalah tentukanlah luas segitiga sama-sisi

keterangan:

panjang AB = Panjang AC = Panjang  .....ketiga sisinya sama panjang

jadi untuk menentukan luas segitiga sama sisi memiliki hubungan erat dengan cara menentukan sudut-sudut trigonometri..?

AB = 6 cm

BC = 6 cm

AC = 6 cm

x = $60^{0}$

Luas Segitiga sama sisi = $\frac{1}{2}$ (AB X AC) . sin x  

Luas Segitiga sama sisi = $\frac{1}{2}$ (6 X 6) . sin $60^{0}$

Luas Segitiga sama sisi = (3 X 6) . $\frac{1}{2}$$\sqrt{3}$

Luas Segitiga sama sisi = (3 X 3).$\sqrt{3}$

Luas Segitiga sama sisi = 9$\sqrt{3}$

jadi, kita bisa menentukan luas segitiga sama sisi dengan mengambil salah satu sudut yang bertemu pada salah satu titik yang menghubungkan kedua garis. 

langkah kedua tentukanlah keliling segitiga sama sisi

keliling segitiga sama sisi adalah jumlah keseluruhan sisi-sisinya:

Keliling Segitiga sama sisi = 6 + 6 + 6 = 18

langkah ketiga tentukanlah nilai S

nilai S adalah setengah dari keliling dari segitiga sama sisi

S = $\frac{K}{2}$

S = $\frac{18}{2}$

S = 9 cm

langkah keempat tentukanlah jari-jari lingkaran dalam segitiga sama sisi

keterangan:

r = jari-jari lingkaran

L = Luas Segitiga sama sisi 

r = $\frac{L}{S}$ 

r = $\frac{9.\sqrt{3}}{9}$

r = $\sqrt{3}$

jadi, jari-jari lingkaran dalam segitiga sama sisi = $\sqrt{3}$.

langkah keempat tentukan keliling lingkaran:

Luas Lingkaran Dalam Segitiga sama sisi = π$r^{2}$

Luas Lingkaran Dalam Segitiga sama sisi =  $\frac{22}{7}$ x $\sqrt{3}^{2}$

Luas Lingkaran Dalam Segitiga sama sisi = $\frac{22}{7}$ x 3

Luas Lingkaran Dalam Segitiga sama sisi = $\frac{66}{7}$ 

contoh soal 19

perhatikan gambar dibawah ini:

diketahui panjang AB = 14 cm, panjang AC = 8 cm, dan panjang BC = 6 cm tentukanlah luas daerah yang tidak diarsir pada segitiga sembarang....?

langkah Pertama tentukanlah keliling segitiga sembarang 

keterangan

Panjang BC = a = 6

Panjang AC = b = 10

Panjang AB = c = 12

keliling segitiga sama sisi adalah jumlah keseluruhan sisi-sisinya:

Keliling Segitiga sama sisi = a + b + c 

Keliling Segitiga sama sisi = 6 + 10 + 12

Keliling Segitiga sama sisi = 28

langkah kedua tentukanlah nilai S

nilai S adalah setengah dari keliling dari segitiga sembarang

S = $\frac{K}{2}$

S = $\frac{28}{2}$

S = 14

langkah ketiga tentukanlah luas segitiga

keterangan:

L = luas segitiga sembarang

a = 6 cm

b = 8 cm

c = 12 cm

S = 14 cm

sehingga

L segitiga  = $\sqrt{S(S-a)(S-b)(S-C)}$

L segitiga = $\sqrt{14(14-6)(14-10)(14-12)}$

L segitiga = $\sqrt{14(8)(4)(2)}$

L segitiga = $\sqrt{(14)(8)(8)}$

L segitiga = 8$\sqrt{14}$

L segitiga = 8 x 3,7

L segitiga = 29,6

langkah keempat tentukanlah jari-jari lingkaran dalam pada Segitiga Sembarang

keterangan:

r = jari-jari lingkaran

L = 29,6

S = 14

r = $\frac{L}{S}$ 

r = $\frac{29,6}{14}$

r = 2,11 cm

luas lingkaran = π$r^{2}$

luas lingkaran = 3,14 x $2,11^{2}$

luas lingkaran = 3,14 x 4,45

luas lingkaran = 13,97

jadi, LuasDaerah yang tidak diarsir................?

Luas Daerah yang tidak diarsir = Luas Segitiga - Luas Lingkaran

Luas Daerah yang tidak diarsir = 29,6 - 13,97

Luas Daerah yang tidak diarsir = 15.63

contoh soal 20

perhatikan gambar dibawah ini:

diketahui jari-jari lingkaran = 7 cm dan Panjang Garis Singgung lingkaran adalah 24 cm. tentukanlah jarak titik pusat dengan titik luar lingkaran ..............?

penyelesaian:

r = 7 cm

BC = 24 cm

OC = jarak titik pusat dengan titik luar lingkaran

OC = .........?

$OC^{2}$ = $BC^{2}$ + $r^{2}$ 

$OC^{2}$ = $24^{2}$ + $7^{2}$ 

$OC^{2}$ = 576 + 49

$OC^{2}$ = 625

OC = $\sqrt{625}$

OC = 25

Jadi, jarak titik pusat dengan titik luar lingkaran = 25 cm

contoh soal 21

Perhatikan gambar dibawah ini:

gambar diatas merupakan segitiga sama kaki. panjang LM = 24 cm, dan panjang LN = 15 cm. tentukanlah luas segitiga LNM....?

penyelesaian:

NO = t  = merupakan tinggi segitiga

LM = a = alas segitiga sama kaki

LN = MN = r

r = 15

a = 24

t =.........?

t = $\sqrt{r^2 - (\frac{1}{2}a)^2}$

t = $\sqrt{15^2 - (\frac{1}{2}24)^2}$

t = $\sqrt{225 - (12)^2}$

t = $\sqrt{225 - 144}$

t = $\sqrt{81}$

t = 9 cm

sehingga:

Luas  $\triangle$LNM= $\frac{1}{2}$ (a x t)

Luas  $\triangle$LNM= $\frac{1}{2}$ (24 x 9)

Luas  $\triangle$LNM= 12 x 9

Luas  $\triangle$LNM= 108 $cm^{2}$

contoh soal 22

diketahui tinggi 8$\sqrt{3}$ dan luas segitiga sama sisi = 64$\sqrt{3}$ tentukanlah panjang sisi segitiga sama sisi.....?

penyelesaian:

t = 8$\sqrt{3}$ $cm^{2}$

luas segitiga sama sisi = 64$\sqrt{3}$

alas = s

s = ... cm.

Luas Segitiga Sama Sisi = $\frac{1}{2}$ alas x tinggi

64$\sqrt{3}$ = $\frac{1}{2}$ (s x t)

64$\sqrt{3}$ = $\frac{1}{2}$ (s x 8$\sqrt{3}$)

64$\sqrt{3}$ = (s x 4$\sqrt{3}$)

(s x 4$\sqrt{3}$) = 64$\sqrt{3}$  ......kedua ruas dibagi akar 3

4s = 64

s = 16 

panjang sisi = 16 cm

contoh soal 23

perhatikan gambar dibawah ini:

tentukanlah luas segitiga $\triangle$KLM...?

penyelesaian:

untuk menyelesaiankan soal diatas ada dua cara yaitu:

panjang AB = k = 20 cm

panjang AC = l = 15 cm

panjang BC = m = 25 cm

Keliling = K

tentukanlah keliling  $\triangle$KLM:

Keliling  $\triangle$KLM = k + l + m

Keliling  $\triangle$KLM  = 20 + 15 + 25

Keliling  $\triangle$KLM  = 60 cm

tentukan nilai S. S merupakan setengah dari keliling $\triangle$KLM

S = $\frac{1}{2}$ Keliling  $\triangle$KLM 

S = $\frac{1}{2}$ x 60

S = 30

terakhir tentukanlah luas $\triangle$ABC:

Luas $\triangle$KLM  = $\sqrt{S(S-k)(S-l)(S-m)}$

Luas $\triangle$KLM = $\sqrt{30(30-20)(30-15)(30-25)}$

Luas  $\triangle$KLM  = $\sqrt{30(10)(15)(5)}$

Luas  $\triangle$KLM  = $\sqrt{(3.10) (10)(15)(5)}$

Luas  $\triangle$KLM  = (10)$\sqrt{(15)(15)}$

Luas  $\triangle$KLM  = 10 x 15

Luas  $\triangle$KLM  = 150

jadi,  $\triangle$KLM  = 150 $cm^2$

contoh soal 24

Perhatikan gambar dibawah ini!

diketahui segitiga siku-siku. panjang AB = 8 cm, panjang AC = 6 cm, dan panjang BC = 10 cm. tentukanlah besar sudut B dengan menggunakan aturan rumus Cosinus...?

jawaban:

AB = x = 8 cm

AC = y = 6 cm

BC = r = 10 cm

Cos $x^0$ = $\frac{x}{r}$

Cos $x^0$ = $\frac{8}{10}$

$x^0$ = $cos^{-1}$ $\frac{8}{10}$

$x^0$ = $cos^{-1}$ (0,8)

$x^0$ = $36,87^0$ 

jadi, $\angle$B = $36,87^0$ 

contoh soal 25

pada gambar dibawah ini:

besar $\angle$M = $76^{0}$ dan $\angle$MLN = $130^{0}$. hitunglah besar $\angle$K....?

Penyelesaian:

untuk menyelesaiakan soal diatas ada dua cara:

cara I:

$\angle$K = $\angle$MLN -  $\angle$M

$\angle$K = $130^{0}$ -  $76^{0}$ 

$\angle$K = $54^{0}$

cara II:

$\angle$KLM = $180^{0}$ - $\angle$MLN

$\angle$KLM = $180^{0}$ -  $130^{0}$ 

$\angle$KLM = $50^{0}$ 

maka

$\angle$K  = $180^{0}$ - ($\angle$M+ $\angle$KLM)

$\angle$K  = $180^{0}$ - ($76^{0}$ + $50^{0}$)

$\angle$K  = $180^{0}$ - $126^{0}$

$\angle$K  = $54^{0}$

contoh soal 26

perhatikan gambar dibawah ini:

diketahui panjang AC = 8 cm, panjang BC = 6 cm, dan panjang AB = 10 cm. tentukanlah panjang garis berat AD pada $\triangle$ABC...?

penyelesaian:

Panjang AC = 8 cm

Panjang BC = 6 cm

Panjang AB = 10 cm

Panjang garis berat AD ..........?

AD = $\sqrt{\frac{(AC)^2 + (AB)^2}{2}-(\frac{1}{2}BC)^2}$

AD = $\sqrt{\frac{(8)^2 + (10)^2}{2}-(\frac{1}{2}(6))^2}$

AD = $\sqrt{\frac{(64 + 100)}{2}-(3)^2}$

AD = $\sqrt{\frac{164}{2}-9}$

AD = $\sqrt{82 - 9}$

AD = $\sqrt{73}$

jadi, panjang garis berat AD = $\sqrt{73}$ cm

contoh soal 27

perhatikan gambar dibawah ini:

diketahui panjang PR = 13 cm, panjang QR = 15 cm, dan panjang PQ = 14 cm. tentukanlah panjang garis bagi RS pada $\triangle$PQR...?

penyelesaian:

Panjang PR = 13 cm

Panjang QR = 15 cm

Panjang PQ = 14 cm

Panjang garis bagi RS ..........?

RS  = $\sqrt{(PR)(QR) \left [ 1-\frac{(PQ)^2}{(PR+QR)^2} \right]}$

RS  = $\sqrt{(13)(15) \left [ 1-\frac{(14)^2}{(13+15)^2} \right]}$

RS  = $\sqrt{(195) \left [ 1-\frac{(14)(14)}{(28)(28)} \right]}$

RS  = $\sqrt{(195) \left [ 1-\frac{(1)(1)}{(2)(2)} \right]}$

RS  = $\sqrt{(195) \left [ 1-\frac{(1)}{(4)} \right]}$

RS  = $\sqrt{(195) \left [\frac{4 - 1}{4} \right]}$

RS  = $\sqrt{(195) \left [\frac{3}{4} \right]}$

RS  = $\sqrt{(3.65) \left [\frac{3}{4} \right]}$

RS  = $\frac{3}{2}$ $\sqrt{65}$

Jadi, panjang garis bagi RS = $\frac{3}{2}$ $\sqrt{65}$

contoh soal 28

perhatikan gambar dibawah ini:

diketahui XY // KL, panjang XM = 8 cm, XY = 6 cm, dan KL = 9 cm, hitunglah panjang KX.............?

penyelesaian:

XM = 8 cm

XY = 6 cm

KL = 9 cm

KM = (8 + KX)

KX = .............?

$\frac{XM}{KM}$ = $\frac{XY}{KL}$

$\frac{8}{8 + KX}$ = $\frac{6}{9}$

$\frac{8}{8 + KX}$ = $\frac{2}{3}$

2 (8 + KX) = 8 x 3

16 + 2KX = 24

2KX = 24 - 16

2KX = 8

KX = $\frac{8}{2}$

KX = 4 cm

contoh soal 29

Seorang nakhoda kapal melihat puncak mercusuar yang berjarak 45 meter dari kapal. Jika diketahui tinggi mercusuar 60 meter, tentukan jarak nakhoda dari puncak mercusuar tersebut!

a. 75 meter

b. 80 meter

c. 90 meter

d. 62 meter

e. 17 meter

penyelesaian:

ilustrasi gambar:

maka jarak nakhoda dari puncak mercusuar dengan menggunakan rumus Teorema Pythagoras:

keterangan:

AB = 45 m

AC= jarak nakhoda dari puncak mercusuar

BC = 60 m

$AB^{2}$ + $BC^{2}$ = $AC^{2}$

$45^{2}$ + $60^{2}$ = $AC^{2}$

2025 + 3600= $AC^{2}$

5625 = $AC^{2}$

$AC^{2}$ = 5625

AC = $\sqrt{5625}$

AC = 75 m

Jadi, jarak nakhoda dari puncak mercusuar  = 75 m

contoh soal 30

seorang pilot sedang terbang melihat ujung landasan dengan sudut depresi 45 derajat. jika ketinggian pesawat 280 meter, tentukan jarak antara ujung landasan dengan titik di tanah yang berada dibawah helkopter...?

a. 75 meter

b. 80 meter

c. 90 meter

d. 62 meter

e. 17 meter

penyelesaian:

ilustrasi gambar:

maka tinggi pohon mangga dapat dihitung dengan menggunakan rumus tan pada trigonometri:

keterangan:

(tan $45^0$ = 1)

BC = x .....sisi yang mengapit sudut x

AB = y .....sisi didepan sudut x

BC = x = 280 meter

tan $x^0$  = $\frac{y}{x}$ 

1 = $\frac{y}{280}$ 

1 x 280 = y

y = 280

maka jarak antara ujung landasan dengan titik di tanah yang berada dibawah helkopter adalah 280 meter

contoh soal 31

perhatikan gambar dibawah ini:

gambar diatas ABCD adalah persegi panjang dan EFGC bujur sangkar. keliling daerah yang diarsir adalah...

a. 40 cm

b. 38 cm

c. 34 cm

d. 32 cm

e. 60 cm

penyelesaian:

perhatikan sisi diatas

keliling daerah yang diarsir = 8 + 12 + (8-6) + 6 + 6 + 6

keliling daerah yang diarsir = 20 + 2 + 18

keliling daerah yang diarsir = 40 cm

Saran dan Kritik Tentang  Soal Latihan Lengkap Bangun Datar 

Kumpulan Soal Latihan Lengkap Bangun Datar.  pembahasan soal latihan mengenai  Bangun Datar. tentunya banyak kekurangan dan kelemahan penulis, penulis banyak berharap kepada para pembaca memberikan kritik saran yang membangun demi sempurnya artikel ini. terimakasih.