Tips Belajar Mudah Trapesium: (Pengertian, Sifat-Sifat, Keliling, Luas, Pembahasan Soal)

 » Pengertian Trapesium

materi kali ini kita akan membahas mengenai trapesium, sebelum kita membahas mengenai trapesium ada banyak yang kita temui dalam kehidupan kita sehari-hari misalnya tas, atap rumah, meja, pondok dan masih banyak contoh lainnya yang belum kita sebutkan. jadi Trapesium adalah Bangun Datar segi empat dengan tepat sepasang sisi yang berhadapan sejajar. untuk lebih jelasnya perhatikan gambar dibawah ini:

» Sifat-sifat Trapesium

perhatikan gambar dibawah ini:

Sifat-sifat Trapesium:

• memiliki sepasang garis yang sejajar

• jumlah sudut yang berdekatan di antara dua sisi sejajar adalah 180⁰

• memiliki dua buah diagonal

» Keliling Trapesium

Keliling Trapesium adalah jumlah keempat panjang sisinya. Dimana terdapat sapang sisi yang  sejajar.

contoh:

keliling trapesium = a + b + c + d

» Luas Trapesium

Luas Trapesium adalah segi empat yang memiliki bidang yang dibatasi oleh sisinya sendiri. untuk menentukan luas Trapesium harus kita tentukan dulu kedua garis yang sejajar dan tinggi trapesium itu sendiri.

Maka rumus luas Trapesium:

Luas Trapesium = ½ (jumlah sisi sejajar) x tinggi

» Pembahasan Soal Trapesium

Perhatikan gambar dibawah ini:

Pada trapezium ABCD disamping, AB sejajar DC, Panjang AD = Panjang BC, sudut ∆A = 75⁰. ∆C = 105⁰. Tentukanlah:

a. sudut ∆B

b. sudut ∆D

c. garis-garis yang sejajar.

Penyelesaian:

a. sudut ∆B

sudut ∆B = ∆A ……….(karena panjang AB = panjang DC)

sudut ∆B = 75⁰.

b. sudut ∆D

sudut ∆D = sudut ∆C …………..( karena panjang AB = panjang DC)

sudut ∆D = 105⁰.

c. garis-garis yang sejajar.

 garis AB // garis CD

keterangan cara baca:

// = sejajar

Perhatikan gambar dibawah ini:

Pada trapesium ABCD disamping, AB sejajar DC, Panjang AD ≠  Panjang BC, sudut ∆A = 65⁰. ∆C = 120⁰. Tentukanlah:

a. sudut ∆B

b. sudut ∆D

c. garis-garis yang sejajar.

Penyelesaian:

a. sudut ∆B

sudut ∆B = 180⁰ – ∆C

sudut ∆B = 180⁰ – 120⁰

sudut ∆B = 60⁰

b. sudut ∆D

sudut ∆D = 180⁰ - ∆A

sudut ∆D = 180⁰ – 65⁰

sudut ∆D = 115⁰ 

gambar dibawah ini adalah trapesium ABCD. 

Tentukanlah keliling trapesium tersebut…?

Penyelesaian:

Keliling trapesium = jumlah keempat sisinya\

Keliling trapesium = Panjang AB + Panjang BC + Panjang CD + Panjang AD

Keliling trapesium = 10 + 7 + 8 + 5

Keliling trapesium = 30

Keliling trapesium = 30 m

Perhatikan gambar dibawah ini:

Tentukanlah keliling trapesium……….?

Penyelesaian:

Untuk menggunakan panjang EB menggunakan teorem Pythagoras:

BC² = EC² + EB²

BC = AD = 5 m

EC = 3 m

5² = 3² + EB²

3² + EB² = 5²

9 + EB² = 25

EB² = 25 – 9

EB² = 16

EB = √16

EB = 4

Maka keliling Trapesium:

Keliling trapesium = AB + BC + CD + AD

CD = 10 m

AD = 5 m

BC = 5 m

AB = 2xEB + DC

AB = 2 x 4 + 10

AB = 8 + 10 = 18 m

Keliling trapesium = 18  + 5 + 5 + 10

Keliling trapesium = 38 m

Perhatikan gambar dibawah ini:

Tentukanlah luas trapesium pada gambar….?

Penyelesaian:

Luas Trapesium = ½ (jumlah sisi sejajar) x tinggi

Panjang AB = 38

Panjang DC = 22

Tinggi = 10

Luas Trapesium = ½ (AB + DC) x t

Luas Trapesium = ½ (38 + 22) x 10

Luas Trapesium = ½ (60) x 10

Luas Trapesium = 30 x 10

Luas Trapesium = 300 m²

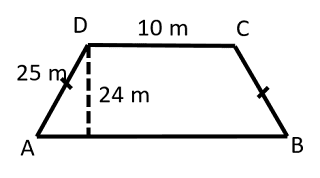
Perhatikan gambar dibawah ini:

Tentukanlah luas trapezium…..?

Penyelesaian:

Tentukanlah panjang AE, menggunakan rumus teorema Pythagoras:

AE² = AD² – DE²

AD = 25

DE = 24

AE² = 25² – 24²

AE² = 625 – 576

AE² = 49

AE = √49

AE = 7

Luas Trapesium = ½ (jumlah sisi sejajar) x tinggi

Panjang AB = 2.AE + DC

Panjang AB = 2x7 + 10

Panjang AB = 24

Panjang DC = 10 m

Tinggi = 24

Luas Trapesium = ½ (24 + 10) x 24

Luas Trapesium = (34) x 12

Luas Trapesium = 408 m²

silahkan kunjungi artikel terkait tentang Bangun Datar: 

Next :