Hubungan Sudut Luar dan Dalam Segitiga

Hello teman-teman kembali lagi kita pada materi Segitiga yaitu: Bagaimana Cara Menentukan hubungan Sudut Luar dan dalam pada Suatu Segitiga,atau sebaliknya hubungan sudut dalam dan luar pada Suatu Segitiga. sebelumnya kita sudah membahas mengenai segitiga siku-siku, segitiga sembarang, segitiga sama kaki, dan segitiga sama sisi. dan sekarang kita akan membahas tuntas hubungan Sudut Luar dan dalam pada Suatu Segitiga. segitiga  merupakan bagian dari macam-macam bangun datar yang memiliki tiga sisi.

Daftar Isi

1. Hubungan Sudut Luar dan Dalam Segitiga 
2. Contoh Soal Hubungan Sudut Luar dan Dalam Segitiga:
3. Saran dan Kritik

Hubungan Sudut Luar dan Dalam Segitiga 

maksud dengan sudut luar pada materi ini adalah sudut yang dibentuh oleh salah satu sisi segitiga dan perpanjangan sisi lainnya.

perhatikan gambar dibawah ini:

keterangan:

$\angle$CBD merupakan sudut luar segitiga.

$\angle$A,$\angle$B, $\angle$C merupakan sudut dalam segitiga.

$\angle$ABC dan $\angle$CBD saling berpelurus maka

$\angle$CBD = $180^{0}$ - $\angle$ABC

$\angle$A + $\angle$B + $\angle$C = $180^{0}$

$\angle$A  = $180^{0}$ - ($\angle$B + $\angle$C)

$\angle$B = $180^{0}$ - ($\angle$A + $\angle$C)

$\angle$C = $180^{0}$ - ($\angle$A + $\angle$B)

maka, hubungan sudut luar dan sudut dalam segitiga:

$\angle$CBD = $\angle$A + $\angle$C

kesimpulan hubungan sudut luar dan sudut dalam segitiga:

besar sudut luar suatu segitiga sama dengan jumlah dua sudut dalam yang tidak berpelurus dengan sudut luar.

Contoh Soal Hubungan Sudut Luar dan Dalam Segitiga:

Contoh Soal 1

pada gambar dibawah ini:

besar $\angle$A = $30^{0}$ dan $\angle$CBD = $120^{0}$. hitunglah besar $\angle$C....?

Penyelesaian:

untuk menyelesaiakan soal diatas ada dua cara:

cara I:

$\angle$C = $\angle$CBD -  $\angle$A

$\angle$C = $120^{0}$ -  $30^{0}$ 

$\angle$C = $90^{0}$

cara II:

$\angle$ABC = $180^{0}$ - $\angle$CBD

$\angle$ABC = $180^{0}$ -  $120^{0}$ 

$\angle$ABC = $60^{0}$ 

maka

$\angle$C  = $180^{0}$ - ($\angle$A + $\angle$B)

$\angle$C  = $180^{0}$ - ($30^{0}$ + $60^{0}$)

$\angle$C  = $180^{0}$ - $90^{0}$

$\angle$C  = $90^{0}$

Contoh Soal 2

pada gambar dibawah ini:

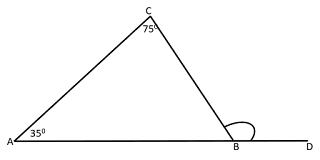
besar $\angle$A = $35^{0}$ dan $\angle$C = $75^{0}$. hitunglah besar $\angle$CBD....?

Penyelesaian:

$\angle$A = $35^{0}$

$\angle$C = $75^{0}$

$\angle$CBD = $\angle$A + $\angle$C

$\angle$CBD = $35^{0}$ + $75^{0}$

$\angle$CBD = $110^{0}$

jadi, $\angle$CBD = $110^{0}$

Contoh Soal 3

pada gambar dibawah ini:

besar $\angle$M = $76^{0}$ dan $\angle$MLN = $130^{0}$. hitunglah besar $\angle$K....?

Penyelesaian:

untuk menyelesaiakan soal diatas ada dua cara:

cara I:

$\angle$K = $\angle$MLN -  $\angle$M

$\angle$K = $130^{0}$ -  $76^{0}$ 

$\angle$K = $54^{0}$

cara II:

$\angle$KLM = $180^{0}$ - $\angle$MLN

$\angle$KLM = $180^{0}$ -  $130^{0}$ 

$\angle$KLM = $50^{0}$ 

maka

$\angle$K  = $180^{0}$ - ($\angle$M+ $\angle$KLM)

$\angle$K  = $180^{0}$ - ($76^{0}$ + $50^{0}$)

$\angle$K  = $180^{0}$ - $126^{0}$

$\angle$K  = $54^{0}$

Contoh Soal 4

pada gambar dibawah ini:

pada gambar tersebut, diketahui $\triangle$ABC sama kaki dengan panjang AB = panjang AC, dan besar $\angle$CAD = $126^{0}$. hitunglah besar $\angle$B....?

Penyelesaian:

$\angle$CAD = $126^{0}$

$\angle$BAC = $180^{0}$ -  $\angle$CAD

$\angle$BAC = $180^{0}$ -  $126^{0}$

$\angle$BAC = $54^{0}$ 

$\angle$A + $\angle$B + $\angle$C = $180^{0}$

Karena  panjang AB = panjang AC maka

$\angle$B =  $\angle$C

$\angle$A = $54^{0}$ 

misalkan 

$\angle$B = x 

$\angle$C = x

$\angle$A + $\angle$B + $\angle$C = $180^{0}$

$54^{0}$  + x + x = $180^{0}$

2x = $180^{0}$ - $54^{0}$ 

2x = $126^{0}$

x = $63^{0}$

jadi,  $\angle$B = $63^{0}$

Contoh Soal 5

pada gambar dibawah ini:

pada gambar tersebut, diketahui $\triangle$ABC  dan besar $\angle$BED = $86^{0}$, $\angle$B = $55^{0}$, dan $\angle$EAC = $70^{0}$. hitunglah besar sudut :

a. $\angle$AEC

b. $\angle$C

c. $\angle$BAE

Penyelesaian:

a. $\angle$AEC

Keterangan:

$\angle$BED = $86^{0}$

$\angle$CED = $180^{0}$ - $86^{0}$

$\angle$CED = $94^{0}$ 

$\angle$AEC = $180^{0}$ -  $94^{0}$ 

$\angle$AEC = $86^{0}$

b. $\angle$C 

keterangan:

$\angle$BED = $86^{0}$

$\angle$CED  = $94^{0}$ 

$\angle$C = $\angle$CED - $\angle$CAE

$\angle$C = $94^{0}$ - $70^{0}$

$\angle$C = $24^{0}$

c. $\angle$BAE

keterangan:

$\angle$BED = $86^{0}$

$\angle$B = $55^{0}$

$\angle$BAE = $\angle$BED - $\angle$B

$\angle$BAE = $86^{0}$ - $55^{0}$

$\angle$BAE = $31^{0}$

Contoh Soal 6

pada gambar berikut, diketahui besar $\angle$SQR = $122^{0}$, $\angle$QRP = $138^{0}$. hitunglah besar $\angle$UPR...?

Penyelesaian:

$\angle$PRQ = $180^{0}$ - $138^{0}$

$\angle$PRQ = $42^{0}$

$\angle$RPQ = $\angle$RQS - $\angle$PRQ

$\angle$PRQ = $122^{0}$ - $42^{0}$

$\angle$PRQ = $80^{0}$

maka:

$\angle$UPR = $180^{0}$ - $\angle$PRQ

$\angle$UPR = $180^{0}$ - $80^{0}$

$\angle$UPR = $100^{0}$ 

Saran dan Kritik

Demikianlah matari mengenai segitiga yaitu Hubungan Sudut Luar dan Dalam Segitiga . materi segitiga merupakan macam-macam Bangun Datar. tentunya banyak kekurangan dan kelemahan penulis, penulis banyak berharap kepada para pembaca memberikan kritik saran yang membangun demi sempurnya artikel ini. terimakasih.

silahkan kunjungi artikel terkait materi Segitiga: