hello teman-teman materi kali ini kita akan membahas latihan soal mengenai
bagaimana cara menentukan Hubungan Sudut pusat dan Sudut Keliling Lingkaran, Rumus Sudut Pusat dan Sudut Keliling, Garis Singgung Persekutuan Luar Dua Lingkaran, Garis Singgung Persekutuan Dalam Dua Lingkaran, Menentukan Luas Lingkaran, Menentukan Keliling Lingkaran, Luas Juring Lingkaran, Luas Tembereng Lingkaran, Menentukan Panjang Busur Lingkaran, Menentukan Panjang Apotema Lingkaran, Menentukan Panjang Tali Busur Lingkaran, Menentukan Panjang Jari-Jari dan Diameter jika hanya Panjang Busur
lingkaran yang diketahui, Menentukan Panjang Jari-Jari dan Diameter jika hanya keliling lingkaran
yang diketahui, Menentukan Panjang Jari-Jari dan Diameter jika hanya luas juring lingkaran
yang diketahui, Menentukan Panjang Jari-Jari dan Diameter jika hanya luas lingkaran yang
diketahui, Menentukan Sudut antara Dua Tali Busur Lingkaran, Menentukan Titik Potong Tali Busur di Luar Lingkaran, Segi Empat Tali Busur dalam Lingkaran Serta Sifat-Sifatnya, Menghitung Luas, Keliling , serta Panjang Jari-Jari Lingkaran dalam Segitiga Siku-Siku, Lingkaran Dalam Segitiga Sama Sisi, Lingkaran Dalam Pada Segitiga Sembarang, Garis Singgung Melalui Titik di Luar Lingkaran.

» Hubungan Sudut pusat dan Sudut Keliling Lingkaran
Sudut Pusat Lingkaran = 2 Sudut Keliling Lingkaran
Sudut Keliling Lingkaran = ½ Sudut Pusat Lingkaran
» Menentukan Sudut antara Dua Tali Busur Lingkaran
$\angle$QTR = $180^{0}$ - ( $\frac{1}{2}$ $\angle$POQ + $\frac{1}{2}$ $\angle$ROS)
$\angle$POQ = menghadap busur PQ
$\angle$ROS = menghadap busur RS
jadi
$\angle$QTP = $\frac{1}{2}$POQ + $\frac{1}{2}$ROS
$\angle$QTP = $\frac{1}{2}$POQ + $\frac{1}{2}$ROS
» Menentukan Titik Potong Tali Busur di Luar Lingkaran
$\angle$ CAT = $\frac{1}{2}$$\angle$AOD
$\angle$ TCA = $180^{0}$ - ($\angle$ CAT + $\angle$ ATC)
maka besar sudut BOC = ... ?
$\angle$ BOC = $180^{0}$ - ($\angle$ TCA + $\angle$ CAT)
$\angle$ATD = $\frac{1}{2}$$\angle$BOC - $\frac{1}{2}$$\angle$AOD
» Segi Empat Tali Busur dalam Lingkaran Serta Sifat-Sifatnya
PR x QS = (PQ x SR) + (PS x QR)
Sudut-Sudut pada Segiempat yang Menghadap Diameter Lingkaran Memiliki Sudut Siku-siku.
Sudut-sudut yang berhadapan pada segiempat tali busur dalam lingkaran akan berjumlah $180^{0}$
» Menghitung Luas, Keliling , serta Panjang Jari-Jari Lingkaran dalam Segitiga Siku-Siku
Luas Segitiga siku-siku = $\frac{1}{2}$ (AB x AC)
Keliling Segitiga Siku-Siku = AB + AC + BC
S = $\frac{K}{2}$
langkah keempat tentukanlah jari-jari lingkaran dalam segitiga siku-siku.
keterangan:
r = jari-jari lingkaran
L = Luas Segitiga siku-siku
S = $\frac{1}{2}$ keliling lingkaran
r = $\frac{L}{S}$
r = $\frac{L}{\frac{1}{2}K}$
» Lingkaran Dalam Segitiga Sama Sisi
Luas Segitiga sama sisi = $\frac{1}{2}$ (AB X AC) . sin x
Luas Segitiga sama sisi = $\frac{1}{2}$ (AC X BC) . sin x
Luas Segitiga sama sisi = $\frac{1}{2}$ (AB X BC) . sin x
Keliling Segitiga Sama Sisi = AB + AC + BC
S = $\frac{K}{2}$
langkah keempat tentukanlah jari-jari lingkaran dalam segitiga sama sisi
keterangan:
r = jari-jari lingkaran
L = Luas Segitiga Sama Sisi
S = $\frac{1}{2}$ keliling lingkaran
» Lingkaran Dalam Pada Segitiga Sembarang
Panjang BC = a
Panjang AC = b
Panjang AB = c
keliling segitiga sama sisi adalah jumlah keseluruhan sisi-sisinya:
Keliling Segitiga sama sisi = a + b + c
langkah kedua tentukanlah nilai S
nilai S adalah setengah dari keliling dari segitiga sembarang
S = $\frac{K}{2}$
langkah ketiga tentukanlah luas segitiga
keterangan:
L = luas segitiga sembaran
a = panjang BC
b = Panjang AC
c = Panjang AB
sehingga:
Lingkaran Dalam Pada Segitiga Sembarang
L = $\sqrt{S(S-a)(S-b)(S-c)}$
langkah keempat tentukanlah jari-jari lingkaran dalam pada Segitiga Sembarang
keterangan:
r = jari-jari lingkaran
L = Luas Segitiga sembarang
S = setengah dari nilai lingkaran
» Garis Singgung Melalui Titik di Luar Lingkaran
keterangan:
r = jari-jari lingkaran
OA = r
OB = r
BC = Panjang Garis Singgung yang melalui Titik Singgung dengan sebuah Titik di Luar Lingkaran
AC = Panjang Garis Singgung yang melalui Titik Singgung dengan sebuah Titik di Luar Lingkaran
OC = Jarak titik pusat lingkaran terhadap titik luar lingkaran
untuk menentukan Panjang Garis Singgung yang melalui Titik Singgung dengan sebuah Titik di Luar Lingkaran tidak terlepas pada rumus teorema pythagoras.
sehingga:
$BC^{2}$ = $OC^{2}$ - $r^{2}$
» Garis Singgung Persekutuan Luar Dua Lingkaran
Keterangan (cara baca):
GSL = Garis singgung persekutuan Luar Dua Lingkaran
JT = jarak titik pusat kedua lingkaran
R = Lingkaran Besar
r = lingkaran kecil
$GSL^{2}$ = $JT^{2}$ - $(R - r)^{2}$
» Garis Singgung Persekutuan Dalam Dua Lingkaran.
Keterangan (cara baca):
GSD = Garis singgung persekutuan dalam Lingkaran
JT = jarak titik pusat lingkaran
R = Lingkaran Besar
r = lingkaran kecil
$GSD^{2}$ = $JT^{2}$ - $(R + r)^{2}$
» Menentukan Luas Tembereng Lingkaran
Keterangan:
π = $\frac{22}{7}$
r = jari-jari lingkaran
d = diameter lingkaran
r = $\frac{1}{2}$d
Rumus Luas Segitiga = $\frac{1}{2}$ alas x tinggi
Rumus Luas Juring Lingkaran = $\frac{x^0}{360^0}$π$r^{2}$
Luas Tembereng Lingkaran = Luas Juring Lingkaran - Luas Segitiga
» Menentukan Luas Lingkaran
Keterangan:
π = $\frac{22}{7}$
r = jari-jari lingkaran
d = diameter lingkaran
r = $\frac{1}{2}$d
luas lingkaran = π$r^{2}$
Luas Lingkaran = π$(\frac{1}{2}d)^{2}$
» Menentukan Keliling Lingkaran
Keterangan :
π = $\frac{22}{7}$
r = jari-jari lingkaran
d = diameter lingkaran
Keliling Lingkaran = 2πr
Keliling Lingkaran = πd
»Luas Juring Lingkaran
Keterangan:
π = $\frac{22}{7}$
r = jari-jari lingkaran
d = diameter lingkaran
x= sudut pusat lingkaran
satu putaran lingkaran = $360^{0}$
r = $\frac{1}{2}$d
Luas Juring Lingkaran = $\frac{x^0}{360^0}$π$r^{2}$
Luas Juring Lingkaran = $\frac{x^0}{360^0}$π$(\frac{1}{2}d)^{2}$
» Menentukan Panjang Busur Lingkaran
Keterangan:
π = $\frac{22}{7}$
r = jari-jari lingkaran
d = diameter lingkaran
x = sudut pusat lingkaran
satu putaran lingkaran = 360 derajat
r = $\frac{1}{2}$d
Panjang Busur Lingkaran = $\frac{x^0}{360^0}$2πr
Panjang Busur Lingkaran = $\frac{x^0}{360^0}$πd
» Panjang Apotema Lingkaran
Rumus Panjang Apotema Lingkaran:
Keterangan:
x = sudut pusat lingkaran
$AB^{2}$ = $AO^{2}$ + $OB^{2}$ - 2(OA)(OB) cos x
untuk menentukan Apotema Lingkaran menggunakan rumus
teorema pythagoras:
$OC^{2}$ = $OA^{2}$ - $OB^{2}$
Keterangan:
π = $\frac{22}{7}$
r = jari-jari lingkaran
d = diameter lingkaran
x = sudut pusat lingkaran
$AB^{2}$ = $AO^{2}$ + $OB^{2}$ - 2(OA)(OB) cos x
» Menentukan Panjang Jari-Jari dan Diameter jika hanya keliling lingkaran
yang diketahui
Rumus Menentukan Panjang Jari-Jari dan Diameter Lingkaran jika hanya keliling
lingkaran yang diketahui
Keterangan:
K = keliling Lingkaran
r = jari-jari lingkaran
d = diamater lingkaran
π = $\frac{22}{7}$
rumus menentukan Jari-jari lingkaran jika hanya keliling lingkaran yang
diketahui:
r = $\frac{K}{2π}$
rumus menentukan Diameter lingkaran jika hanya keliling lingkaran yang
diketahui:
r = $\frac{K}{πd}$
» Menentukan Panjang Jari-Jari dan Diameter jika hanya Panjang Busur lingkaran
yang diketahui
Keterangan:
π = $\frac{22}{7}$
r = jari-jari lingkaran
d = diameter lingkaran
x = sudut pusat lingkaran
360 = satu putaran lingkaran
PB = Panjang Busur Lingkaran rumus menentukan Jari-jari lingkaran jika hanya
Panjang Busur yang diketahui:
r = $\frac{360^0.PB}{2x^0.π}$
» Menentukan Panjang Jari-jari dan Diameter jika hanya Luas Lingkaran yang
diketahui
Keterangan:
π = $\frac{22}{7}$
r = jari-jari lingkaran
d = diameter lingkaran
r = $\frac{1}{2}$d
L = Luas Lingkaran
rumus menentukan Jari-jari lingkaran jika hanya Luas Lingkaran yang
diketahui:
$r^{2}$= $\frac{L}{π}$
r = $\sqrt{\frac{L}{π}}$
» Menentukan Panjang Jari-jari dan Diameter Lingkaran jika hanya Luas Juring
Diketahui
Keterangan:
π = $\frac{22}{7}$
r = jari-jari lingkaran
d = diameter lingkaran
x = sudut pusat lingkaran
360 = satu putaran lingkaran
r = $\frac{1}{2}$d
LJ = Luas Juring Lingkaran
Rumus Menentukan Panjang Jari-jari Lingkaran jika hanya luas juring diketahui
r = $\sqrt{\frac{LJ.360^0}{x^0.π}}$
Latihan Soal Lengkap Pertama Lingkaran
1. Ayah akan membuat taman berbentuk lingkaran dengan jari-jari 35 m. Di
sekeliling taman akan ditanami pohon cemara dengan jarak 1 m. Jika satu pohon
memerlukan biaya Rp25.000,00, seluruh biaya penanaman pohon cemara adalah….
A. Rp5.900.000,00
B. Rp5.700.000,00
C. Rp5.500.000,00
D. Rp5.200.000,00
jawaban:
Keliling lingkaran = 2πr = 2 × $\frac{22}{7}$ 35 = 220
Banyak pohon cemara di sekeliling taman = 220 : 1 × 1 = 220
Seluruh biaya penanaman pohon cemara = 220 × 25.000 = 5.500.000
Jadi seluruh biaya penanaman pohon cemara adalah Rp5.500.000,00
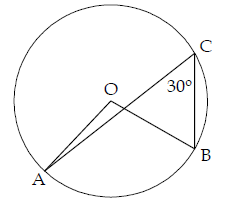
2. Perhatikan gambar di samping ini! Diketahui O adalah titik pusat
lingkaran. Besar sudut AOB adalah ….
A. 15°
B. 30°
C. 45°
D. 60°
jawaban:
Ingat kembali sifat sudut keliling dan sudut pusat lingkaran yang menghadap
ke busur yang sama bahwa besar sudut pusat adalah dua kali besar sudut
keliling. Perhatikan bahwa O pusat lingkaran, C sebuah titik pada lingkaran
serta $\angle$AOB dan
$\angle$ACB sama-sama menghadap busur AB. Dengan demikian
$\angle$AOB = 2 × $\angle$ACB
$\angle$AOB = 2 × 30°
$\angle$AOB = 60°
Jadi besar sudut AOB adalah 60°
3. Keliling sebuah lingkaran 396 cm. Jika π = $\frac{22}{7}$, maka panjang
jari-jari lingkaran tersebut adalah …
A. 36 cm
B. 26 cm
C. 63 cm
D. 126 cm
jawaban:
keterangan:
Keliling Lingkaran = 396
π = $\frac{22}{7}$
Keliling lingkaran = 2πr
396 = 2$\frac{22}{7}$r
396 x 7 = 44r .............................. kedua ruas dibagi 44
$\frac{396.7}{44}$ = $\frac{44}{44}$r
9 x 7 = r
r = 63 cm
jadi, panjang jari-jari lingkaran = 63 cm
4. Panjang busur lingkaran di hadapan sudut pusat $45^{0}$ dan jari-jari
lingkaran itu 28 cm dengan $\frac{22}{7}$ adalah …
A. 11 cm
B. 22 cm
C. 44 cm
D. 88 cm
jawaban:
keterangan:
r = 28 cm
π = $\frac{22}{7}$
x = $45^{0}$
Panjang Busur Lingkaran = $\frac{x}{360^{0}}$2πr
Panjang Busur Lingkaran = $\frac{45^{0}}{360^{0}}$(2)$\frac{22}{7}$(28)
Panjang Busur Lingkaran = $\frac{1}{8}$(44 x 4)
Panjang Busur Lingkaran = $\frac{1}{2}$44
Panjang Busur Lingkaran = 22 cm
5. Dua buah lingkaran masing-masing berpusat di A dan B dengan jari-jari 5
cm dan 3 cm. Jika jarak kedua pusat lingkaran itu 17 cm, maka panjang garis
singgung persekutuan dalamnya adalah …
A. 8 cm
B. 12 cm
C. 14 cm
D. 15 cm
jawaban:
iketahui:
R = 5 cm
r = 3 cm
jarak titik pusat kedua lingkaran (panjang AB) disimbolkan JT.
JT = 17
Sehingga GSD………..?
$GSD^{2}$ = $JT^{2}$ - $(R + r)^{2}$
$GSD^{2}$ = $17^{2}$ - $(5 + 3)^{2}$
$GSD^{2}$ = 289 - $(8)^{2}$
$GSD^{2}$ = 289 - 64
$GSD^{2}$ = 225
GSD = $\sqrt{225}$
GSD = 15
Jadi, panjang Garis Singgung Persekutan dalamnya = 15 cm
6. Jika luas sebuah lingkaran 38,5 $cm^{2}$ dan π = $\frac{22}{7}$, maka
jari-jari lingkaran tersebut adalah …
A. 3,5 cm
B. 12,3 cm
C. 12,5 cm
D. 6,1 cm
jawaban:
π = $\frac{22}{7}$
r = ..............?
r = $\frac{1}{2}$d
L = 38,5 $cm^{2}$
rumus menentukan Jari-jari lingkaran jika hanya Luas Lingkaran yang
diketahui:
$r^{2}$= $\frac{L}{π}$
r = $\sqrt{\frac{L}{π}}$
r = $\sqrt{\frac{38,5}{\frac{22}{7}}}$
r = $\sqrt{\frac{38,5}{3,14}}$
r = $\sqrt{12,26}$
r = 3,50
jadi, panjang jari-jari lingkaran adalaha 3,50 cm
7. Perhatikan gambar lingkaran di samping $\angle$AOB = 45°, OA = 8 dm dan π
= 3,14. Luas juring AOB adalah ...
A. 6,28 $dm^{2}$
B. 25,12 $dm^{2}$
C. 50,24 $dm^{2}$
D. 100,48 $dm^{2}$
Keterangan:
π = $\frac{22}{7}$
r = 8 dm
x = sudut pusat lingkaran
360 = satu putaran lingkaran
Luas Juring Lingkaran = $\frac{x^0}{360^0}$π$r^{2}$
Luas Juring Lingkaran = $\frac{45^0}{360^0}$(3,14)$8^{2}$
Luas Juring Lingkaran = $\frac{1}{8}$(3,14)$8^{2}$
Luas Juring Lingkaran = 8 x 3,14
Luas Juring Lingkaran = 25,12
luas juring lingkaran = 25,12 $dm^{2}$
8. Dua buah lingkaran dengan panjang jari-jarinya 11 cm dan 2 cm, berpusat
di A dan B. Jika panjang garis singgung persekutuan luarnya 12 cm, maka jarak pusat kedua lingkaran
tersebut adalah …
A. 10 cm
B. 13 cm
C. 14 cm
D. 15 cm
jawaban:
Diketahui:
R =11 cm
r = 2 cm
jarak titik pusat kedua lingkaran (panjang AB)
disimbolkan JT.
JT = …….. cm
GSL = 12 cm
Sehingga JT………..?
$GSL^{2}$ = $JT^{2}$ - $(R - r)^{2}$
$12^{2}$ = $JT^{2}$ - $(11 - 2)^{2}$
144 = $JT^{2}$ - $(9)^{2}$
144 = $JT^{2}$ - 81
$JT^{2}$ = 144 + 81
$JT^{2}$ = 225
JT = $\sqrt{225}$
JT = 15
Jadi, jarak pusat kedua lingkaran = 15 cm
9. Pada gambar di samping panjang busur AB dihadapan sudut $30^{0}$ besar
sudut AOB adalah …
A. 5,1 cm
B. 7,3 cm
C. 10,2 cm
D. 14,6 cm
jawaban:
π = $\frac{22}{7}$
r = 14 cm
x = $30^{0}$
360 = satu putaran lingkaran
Panjang Busur AB = $\frac{x^0}{360^0}$.2πr
Panjang Busur AB = $\frac{30^0}{360^0}$.2.$\frac{22}{7}$.14
Panjang Busur AB = $\frac{1}{12}$.2.$\frac{22}{7}$.14
Panjang Busur AB = $\frac{1}{6}$ x 44
Panjang Busur AB = 7,3
10. Panjang garis singgung persekutuan luar CD pada gambar di samping adalah
16 cm. Jika panjang AB = 20 cm dan BC = 4 cm, maka panjang AD adalah …
A. 20 cm
B. 18 cm
C. 16 cm
D. 14 cm
jawaban:
Diketahui:
R = AD = …. cm
r = BC = 4 cm
jarak titik pusat kedua lingkaran (panjang AB)
disimbolkan JT.
JT = jarak titik pusat = AB = 20 cm
GSL = 16 cm
maka:
$GSL^{2}$ = $JT^{2}$ - $(R - r)^{2}$
$16^{2}$ = $20^{2}$ - $(R - 4)^{2}$
256 = 400 - $(R - 4)^{2}$
$(R - 4)^{2}$ = 400 - 256
$(R - 4)^{2}$ = 144
(R - 4) = $\sqrt{144}$
R = 12 + 4
R = 16
maka,
panjang AD = 16 cm
11. Jari-jari lingkaran yang luasnya 2464 $cm^{2}$ dengan
pendekatan π = $\frac{22}{7}$ adalah …
A. 14 cm
B. 22 cm
C. 28 cm
D. 98 cm
jawaban:
Keterangan:
π = $\frac{22}{7}$
r = ..............?
L = 2464 $cm^{2}$
rumus menentukan Jari-jari lingkaran jika hanya Luas Lingkaran yang
diketahui:
$r^{2}$= $\frac{L}{π}$
r = $\sqrt{\frac{L}{π}}$
r = $\sqrt{\frac{2464}{\frac{22}{7}}}$
r = $\sqrt{\frac{2464.7}{22}}$
r = $\sqrt{112.7}$
r = $\sqrt{784}$
r = 28
jadi, panjang jari-jari lingkaran adalaha 28 cm
12. Perhatikan gambar di bawah. Bila panjang PQ = 17 cm, PM = 5 cm dan QN = 3
cm, maka panjang MN adalah …
A. 9 cm M
B. 12 cm
C. 14 cm
D. 15 cm
jawaban:
R = PM = 5 cm
r = QN = 3 cm
jarak titik pusat kedua lingkaran (panjang PQ) disimbolkan JT.
JT = 17
Sehingga GSD………..?
$GSD^{2}$ = $JT^{2}$ - $(R + r)^{2}$
$GSD^{2}$ = $17^{2}$ - $(5 + 3)^{2}$
$GSD^{2}$ = 289 - $(8)^{2}$
$GSD^{2}$ = 289 - 64
$GSD^{2}$ = 225
GSD = $\sqrt{225}$
GSD = 15
Jadi, panjang Garis Singgung Persekutan dalamnya = 15 cm
13. Dua buah lingkaran berjari-jari masing-masing 7 cm dan 1 cm. Jika jarak
antara kedua pusat lingkaran itu 10 cm, maka panjang garis singgung
persekutuan luar kedua lingkaran adalah …
A. 6 cm
B. 8 cm
C. 11,7 cm
D. 12,8 cm
Jawaban:
R = 7 cm
r = 1 cm
jarak titik pusat kedua lingkaran (panjang AB)
disimbolkan JT.
JT = 10 cm
Sehingga GSL………..?
$GSL^{2}$ = $JT^{2}$ - $(R - r)^{2}$
$GSL^{2}$ = $10^{2}$ - $(7 - 1)^{2}$
$GSL^{2}$ = 100 - 36
$GSL^{2}$ = 64
GSL = $\sqrt{64}$
GSL = 8
Jadi, garis singgung persekutuan luar dua lingkaran = 8 cm
14. Gambar di samping Δ ABC siku-siku di A dan lingkaran dalam terpusat di
M. Bila AB = 8 cm dan AC = 6 cm, luas lingkaran yang berpusat di M adalah
A. 5π $cm^{2}$
B. 4π $cm^{2}$
C. 3π $cm^{2}$
D. 2π $cm^{2}$
jawaban:
Δ ABC
AB = 8 cm
AC = 6 cm
$BC^{2}$ = $AB^{2}$ + $AC^{2}$
$BC^{2}$ = $8^{2}$ + $6^{2}$
$BC^{2}$ = 64 + 36
$BC^{2}$ = 100
BC = $\sqrt{100}$
BC = 10 cm
luas ABC = $\frac{1}{2}$ x alas x tinggi
luas ABC = $\frac{1}{2}$ x AB x AC
luas ABC = $\frac{1}{2}$ x 8 x 6
luas ABC = 24 $cm^{2}$,
keliling segitiga = AB + AC + BC
keliling segitiga = 8 + 6 + 10
keliling segitiga = 24
s = $\frac{1}{2}$ x keliling segitiga
s = $\frac{1}{2}$ x 24
s = 12 cm
sehingga, jari-jari lingkaran dalam segitiga
r = $\frac{luas segitiga ABC}{s}$
r = $\frac{24}{12}$
r = 2 cm
maka:
luas lingkaran = π$r^{2}$
luas lingkaran = π$2^{2}$
luas lingkaran = 4π $cm^{2}$
15. Seorang pelari mengelilingi lapangan berbentuk lingkaran sebanyak 5
kali dengan menempuh jarak 1.320 m.luas lapangan tersebut adalah …
A. 254 $m^{2}$
B. 2.772 $m^{2}$
C. 5.544 $m^{2}$
D. 6.600 $m^{2}$
Jawaban:
K = 1.320 m
total keliling 5 kali mengelilingi lingkaran
K = 1.320 m
r = jari-jari lingkaran
π = $\frac{22}{7}$
rumus menentukan Jari-jari lingkaran jika hanya keliling lingkaran yang
diketahui:
r = $\frac{1320}{2π}$
r = $\frac{1320}{2\frac{22}{7}}$
r = $\frac{1320}{\frac{44}{7}}$
r = 1320 x ${\frac{7}{44}}$
r = 30 x 7
r = 210
jadi, luas lapangan .....
luas lapangan = π$r^{2}$
luas lapangan = $\frac{22}{7}$(210)(210)
Luas Lapangan = 22 x 30 x 210
Luas Lapangan = 138.600
sehingga luas lapangan = 138.600 $m^{2}$
16. perhatikan gambar dibawah ini...?
Segi Empat Tali Busur dalam Lingkaran. AOB adalah garis tengah. Jika besar $\angle$ABC = $63^{0}$ dan besar $\angle$ABD = $49^{0}$, $\angle$ CAD = …
A. $27^{0}$
B. $41^{0}$
C. $68^{0}$
D. $90^{0}$
penyelesaian:
$\angle$ABC = $63^{0}$
$\angle$ABD = $49^{0}$
$\angle$ACB dan $\angle$ADB merupakan sudut siku-siku. karena kedua sudut Sudut-Sudut pada Segiempat yang Menghadap Diameter Lingkaran Memiliki Sudut Siku-siku.
$\angle$ACB = $90^{0}$
$\angle$ADB = $90^{0}$
ditanya: sudut CAD = …..?
$\angle$CAD = $\angle$CAB + $\angle$DAB
Langkah pertama tentukan sudut CAB
$\angle$CAD = $180^{0}$ - ($\angle$ACB + $\angle$ABC)
$\angle$CAD = $180^{0}$ - ($90^{0}$ + $63^{0}$)
$\angle$CAD = $180^{0}$ - $153^{0}$
$\angle$CAD = $27^{0}$
Langkah kedua tentukan sudut DAB
$\angle$DAB = $180^{0}$ - ($\angle$ADB + $\angle$ABD)
$\angle$DAB = $180^{0}$ - ($90^{0}$ + $49^{0}$)
$\angle$DAB = $180^{0}$ - $139^{0}$
$\angle$DAB = $41^{0}$
Sehingga
$\angle$CAD = $\angle$CAB + $\angle$DAB
$\angle$CAD = $27^{0}$ + $41^{0}$
$\angle$CAD = $68^{0}$
jadi, $\angle$CAD = $68^{0}$
17. perhatikan gambar dibawah ini...?
diketahui O adalah titik pusat lingkaran, besar sudut AOB adalah...
A. $15^{0}$
B. $30^{0}$
C. $45^{0}$
D. $60^{0}$
E. $65^{0}$
Penyelesaian:
sudut pusat lingkaran = $\angle$AOB
Sudut keliling lingkaran = $\angle$ACB
$\angle$ACB =$30^{0}$
sudut pusat lingkaran = 2 x sudut keliling lingkaran
$\angle$AOB = 2 x $\angle$ACB
$\angle$AOB = 2 x $30^{0}$
$\angle$AOB = $60^{0}$
18. perhatikan gambar dibawah ini...?

diketahui jari-jari lingkaran adalah 14 cm. Luas Tembereng yang diarsir adalah ....
A. 126 $cm^{2}$
B. 127 $cm^{2}$
C. 82 $cm^{2}$
D. 92 $cm^{2}$
E. 54 $cm^{2}$
penyelesaian:
r = 14 cm
x = sudut pusat lingkaran
x = $90^{0}$
rumus menentukan luas tembereng lingkaran yaitu:
Luas Tembereng Lingkaran = Luas Juring Lingkaran - Luas Segitiga
langkah pertama tentukan luas juring lingkaran ...?
Luas Juring Lingkaran = $\frac{x^0}{360^0}$π$r^{2}$
Luas Juring Lingkaran = $\frac{90^0}{360^0}$ x $\frac{22}{7}$ x $14^{2}$
Luas Juring Lingkaran = $\frac{1}{4}$ x $\frac{22}{7}$ x (14 x 14)
Luas Juring Lingkaran = $\frac{1}{2}$ x (11 x 2 x 14)
Luas Juring Lingkaran = 11 x 14
Luas Juring Lingkaran = 154 $cm^{2}$
tahap kedua tentukan luas segitiga..?
untuk menentukan luas segitiga sama sisi kita menggunakan konsep rumus luas trigonometri sinus.
Luas segitiga = $\frac{1}{2}$ x r x r sin x
Luas segitiga = $\frac{1}{2}$ x 12 x 12 $90^{0}$
Luas segitiga = 6 x 12 x 1
Luas segitiga = 72 $cm^{2}$
sehingga:
Luas Tembereng Lingkaran = Luas Juring Lingkaran - Luas Segitiga
Luas Tembereng Lingkaran = 154 $cm^{2}$ - 72 $cm^{2}$
Luas Tembereng Lingkaran = 82 $cm^{2}$
jadi, luas tembereng lingkaran = 82 $cm^{2}$
Demikianlah matari mengenai Latihan Soal Lengkap Pertama
lingkaran. materi
lingkaran merupakan unsur-unsur bangun datar. tentunya banyak
kekurangan dan kelemahan penulis, penulis banyak berharap kepada para
pembaca memberikan kritik saran yang membangun demi sempurnya artikel ini.
terimakasih.
silahkan kunjungi artikel terkait tentang
Lingkaran :
















Post a Comment for "Latihan Soal Lengkap Pertama Lingkaran "