Kumpulan Soal Latihan Lengkap pada Segitiga

Hello teman-teman kembali lagi kita pada materi Segitiga yaitu: kumpulan soal Latihan Lengkap Segitiga. segitiga merupakan bangun datar yang memiliki tiga sisi. dan tiga buah sudut.

Indikator Kumpulan Soal Latihan Lengkap Segitiga 

indikator-indikator kumpulan soal Latihan Lengkap Segitiga yaitu:

• Menentukan Garis Bagi Pada Segitiga 
• menghitung Perbandingan Segmen garis pada Segitiga
• Menentukan Titik Berat Pada Segitiga Sembarang
• Menentukan Titik Berat Pada Segitiga Sama Kaki
• Menentukan Titik Berat Pada Segitiga Sama Sisi
• Menentukan Titik Berat Pada Segitiga Siku-Siku
• Menentukan Panjang Garis Berat Suatu Segitiga
• menghitung Hubungan Besar Sudut dan Panjang Sisi Suatu Segitiga
• menghitung Hubungan Panjang dari Ketiga Sisi Segitiga
• Menentukan Besar Sudut Segitiga Semberang Menggunakan Aturan Cosinus
• Menentukan Panjang Sisi Segitiga dengan Rumus Sinus
• Penerapan Teorema Pythagoras atau Segitiga Siku-siku Dalam Kehidupan Sehari-hari
• Menghitung Hubungan Sudut Luar dan Dalam Segitiga
• Menentukan Panjang Jari-Jari Lingkaran dalam pada Segitiga Sembarang
• Menentukan Keliling Lingkaran Dalam pada Segitiga Sembarang
• Menentukan Luas Lingkaran Dalam pada Segitiga Sembarang
• Menentukan Luas Lingkaran Luar Pada Segitiga Sembarang
• Menentukan Panjang Jari-Jari Lingkaran Dalam Segitiga Sama Sisi
• Menentukan Keliling Lingkaran Dalam Segitiga Sama Sisi
• Menentukan Luas Lingkaran Dalam Segitiga Sama Sisi
• Menentukan Luas Lingkaran Luar Segitiga Sama Sisi
• Menentukan Besar Sudut Segitiga Siku-Siku Menggunakan Aturan Trigonometri
• Menentukan Panjang Jari-Jari Lingkaran dalam Segitiga Siku-Siku
• Menentukan Keliling Lingkaran Dalam Segitiga Siku-Siku
• Menentukan Luas Lingkaran Dalam Segitiga Siku-Siku
• Menentukan Luas Lingkaran Luar Segitiga Siku-Siku
• Menentukan Tinggi Segitiga Sembarang
• Menentukan Keliling Segitiga Sembarang
• Menentukan Luas Segitiga Sembarang 
• Menentukan Tinggi Segitiga Sama Kaki
• Menentukan Keliling Segitiga Sama Kaki
• Menentukan Luas Segitiga Sama Kaki
• Menentukan Panjang Salah Satu Sisi Yang Tidak Diketahui pada segitiga sama kaki
• Menentukan Tinggi Segitiga Sama Sisi
• Menentukan Keliling Segitiga Sama Sisi
• Menentukan Luas Segitiga Sama Sisi
• Menentukan Panjang Salah Satu Sisi Yang Tidak Diketahui pada segitiga sama sisi
• Soal Latihan Fungsi Trigonometri pada Segitiga serta Penerapannya Dalam Kehidupan Sehari-hari

Materi Kumpulan Soal Latihan Lengkap pada Segitiga

Loading....

Kumpulan Soal Latihan Lengkap pada Segitiga

1. perhatikan gambar dibawah ini:

tentukanlah Luas lingkaran dalam segitiga siku-siku...........?

penyelesaian:

tahap I tentukanlah luas segitiga siku-siku

Luas Segitiga siku-siku = $\frac{1}{2}$ alas x tinggi

alas segitiga siku-siku = panjang AB = 40 cm

tinggi segitiga siku-siku = Panjang AC = 30 cm

Luas Segitiga siku-siku = $\frac{1}{2}$ x 40 x 30

Luas Segitiga Siku-Siku = 20 x 30

Luas Segitiga Siku-Siku = 600 $cm^{2}$

tahap II tentukanlah keliling segitiga siku-siku

K = AB + AC + BC

AB = 40 cm

AC = 30 cm

BC = ...........? untuk menentukan panjang YZ menggunakan rumus teorema pythagoras...?

$BC^{2}$ = $AB^{2}$ + $AC^{2}$

$BC^{2}$ = $40^{2}$ + $30^{2}$

$BC^{2}$ = 1600 + 900

$BC^{2}$ = 2500

BC = $\sqrt{2500}$

YZ = 50

K = 30 + 40 + 50

K = 120

tahap III tentukan nilai S

S = $\frac{120}{2}$ = 60 cm

tahap IV tentukan jari-jari lingkaran

keterangan

L = 600 $cm^{2}$

S = 60 cm

r = $\frac{L}{S}$ 

r = $\frac{600}{60}$ 

r = 10 cm

jadi, panjang jari-jari lingkaran dalam segitiga = 10 cm

Sehingga 

keterangan:

r = 10

π = 3,14

Luas Lingkaran Dalam Segitiga Siku-Siku = π$r^{2}$

Luas Lingkaran Dalam Segitiga Siku-Siku =   3,14 x $10^{2}$

Luas Lingkaran Dalam Segitiga Siku-Siku = 3,14 x 100

Luas Lingkaran Dalam Segitiga Siku-Siku = 314 $cm^{2}$

2. perhatikan gambar dibawah ini:

diketahui panjang sisi segitiga sama = 6 cm. tentukanlah luas lingkaran dalam segitiga sama sisi............?

Langkah Pertama adalah tentukanlah luas segitiga sama-sisi

keterangan:

panjang AB = Panjang AC = Panjang  .....ketiga sisinya sama panjang

jadi untuk menentukan luas segitiga sama sisi memiliki hubungan erat dengan cara menentukan sudut-sudut trigonometri..?

AB = 6 cm

BC = 6 cm

AC = 6 cm

x = $60^{0}$

Luas Segitiga sama sisi = $\frac{1}{2}$ (AB X AC) . sin x  

Luas Segitiga sama sisi = $\frac{1}{2}$ (6 X 6) . sin $60^{0}$

Luas Segitiga sama sisi = (3 X 6) . $\frac{1}{2}$$\sqrt{3}$

Luas Segitiga sama sisi = (3 X 3).$\sqrt{3}$

Luas Segitiga sama sisi = 9$\sqrt{3}$

jadi, kita bisa menentukan luas segitiga sama sisi dengan mengambil salah satu sudut yang bertemu pada salah satu titik yang menghubungkan kedua garis. 

langkah kedua tentukanlah keliling segitiga sama sisi

keliling segitiga sama sisi adalah jumlah keseluruhan sisi-sisinya:

Keliling Segitiga sama sisi = 6 + 6 + 6 = 18

langkah ketiga tentukanlah nilai S

nilai S adalah setengah dari keliling dari segitiga sama sisi

S = $\frac{K}{2}$

S = $\frac{18}{2}$

S = 9 cm

langkah keempat tentukanlah jari-jari lingkaran dalam segitiga sama sisi

keterangan:

r = jari-jari lingkaran

L = Luas Segitiga sama sisi 

r = $\frac{L}{S}$ 

r = $\frac{9.\sqrt{3}}{9}$

r = $\sqrt{3}$

jadi, jari-jari lingkaran dalam segitiga sama sisi = $\sqrt{3}$.

langkah keempat tentukan keliling lingkaran:

Luas Lingkaran Dalam Segitiga sama sisi = π$r^{2}$

Luas Lingkaran Dalam Segitiga sama sisi =  $\frac{22}{7}$ x $\sqrt{3}^{2}$

Luas Lingkaran Dalam Segitiga sama sisi = $\frac{22}{7}$ x 3

Luas Lingkaran Dalam Segitiga sama sisi = $\frac{66}{7}$ 

3. perhatikan gambar dibawah ini:

diketahui panjang AB = 15 cm, panjang AC = 13 cm, dan panjang BC = 6 cm tentukanlah keliling lingkaran dalam pada segitiga sembarang...?

langkah Pertama tentukanlah keliling segitiga sembarang

keterangan

Panjang BC = a = 6

Panjang AC = b = 13

Panjang AB = c = 15

keliling segitiga sama sisi adalah jumlah keseluruhan sisi-sisinya:

Keliling Segitiga sama sisi = a + b + c 

Keliling Segitiga sama sisi = 6 + 13 + 15

Keliling Segitiga sama sisi = 34 

langkah kedua tentukanlah nilai S

nilai S adalah setengah dari keliling dari segitiga sembarang

S = $\frac{K}{2}$

S = $\frac{34}{2}$

S = 17

langkah ketiga tentukanlah luas segitiga

keterangan:

L = luas segitiga sembarang

a = 6

b = 13

c = 15

sehingga

L = $\sqrt{S(S-a)(S-b)(S-C)}$

L = $\sqrt{17(17-6)(17-13)(17-14)}$

L = $\sqrt{17(11)(4)(3)}$

L = $\sqrt{(187)(12)}$

L = $\sqrt{2244}$

L = 47,37 $cm^{2}$

langkah keempat tentukanlah jari-jari lingkaran dalam pada Segitiga Sembarang

keterangan:

r = jari-jari lingkaran

L = 47,37 $cm^{2}$

S = 17

r = $\frac{L}{S}$ 

r = $\frac{47,37}{17}$ 

r = 2,79 cm

jadi, Keliling Lingkaran ......?

r = 2,79

π = 3,14

Keliling lingkaran = 2(2,79) (3,14)

Keliling lingkaran = 2(2,79) (3,14)

Keliling lingkaran = 17,52

4. perhatikan gambar dibawah ini:

gambar diatas merupakan segitiga sama kaki. panjang AB = 12 cm, dan panjang AC = 10 cm. tentukanlah panjang tinggi segitiga ABC....?

penyelesaian:

titik tengah Panjang AB beri nama titik D sehingga tinggi segitiga ABC tegak lurus dengan alasnya.

Panjang CD = t

AB = a = alas segitiga

AC = BC = r

a = 16 cm

r = 10 cm

sehingga untuk menentukan Tinggi $\triangle$ABC menggunakan teorema pythagoras:

t = $\sqrt{r^2 - (\frac{1}{2}a)^2}$

t = $\sqrt{10^2 - (\frac{1}{2}.12)^2}$

t = $\sqrt{100 - (6)^2}$

t = $\sqrt{100 - 36}$

t = $\sqrt{64}$

t = 8

jadi tinggi segitiga ABC = 8 cm

5. Perhatikan gambar dibawah ini:

diketahui panjang AB = 20 cm, tentukanlah luas segitiga sama sisi.....?

penyelesaian:

AB = 20 cm

s = 20 cm.

tahap I tentukan tinggi segitiga:

t = $\sqrt{s^2 - (\frac{1}{2}s)^2}$

t = $\sqrt{20^2 - (\frac{1}{2}.(20))^2}$

t = $\sqrt{400 - 10^2}$

t = $\sqrt{400 - 100}$

t = $\sqrt{300}$

t = 10$\sqrt{3}$

tahap II tentukan luas segitiga:

alas = s = 20 cm

t = 10$\sqrt{3}$

Luas Segitiga Sama Sisi = $\frac{1}{2}$ alas x tinggi

Luas Segitiga Sama Sisi = $\frac{1}{2}$ (20 x 10$\sqrt{3}$)

Luas Segitiga Sama Sisi = $\frac{1}{2}$ (200$\sqrt{3}$)

Luas Segitiga Sama Sisi = 100$\sqrt{3}$

Jadi, luas segitiga sama sisi adalah 100$\sqrt{3}$

6. panjang tiga buah garis masing-masing adalah 5 cm, 7,5 cm, 6,5 cm. apakah ketiga sisi tersebut dapat membentuk segitiga.....?

Panjang sisi I = 5 cm

Panjang sisi II = 7,5 cm

Panjang sisi III = 6,5 cm

penyelesaian:

Pembuktian:

Panjang sisi I = 5 cm

7,5 + 6,5 terbukti bahwa lebih panjang dari 5 cm

Panjang sisi II = 7,5 cm

5 + 6,5 terbukti bahwa lebih panjang dari 7,5 cm

Panjang sisi III = 6,5 cm

5 + 7,5  terbukti bahwa lebih panjang dari 6,5 cm

Karena jumlah panjang dua buah garis  selalu melebihi panjang sisi ketiga, maka ketiga garis tersebut dapat membentuk segitiga.

7. pada gambar dibawah ini:

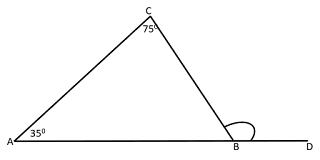
besar $\angle$A = $35^{0}$ dan $\angle$C = $75^{0}$. hitunglah besar $\angle$CBD....?

Penyelesaian:

$\angle$A = $35^{0}$

$\angle$C = $75^{0}$

$\angle$CBD = $\angle$A + $\angle$C

$\angle$CBD = $35^{0}$ + $75^{0}$

$\angle$CBD = $110^{0}$

jadi, $\angle$CBD = $110^{0}$

8. perhatikan gambar dibawah ini:

diketahui panjang AC = 8 cm, panjang BC = 6 cm, dan panjang AB = 10 cm. tentukanlah panjang garis berat CD pada $\triangle$ABC...?

penyelesaian:

Panjang AC = 8 cm

Panjang BC = 6 cm

Panjang AB = 10 cm

Panjang garis berat CD ..........?

CD = $\sqrt{\frac{(AC)^2 + (BC)^2}{2}-(\frac{1}{2}AB)^2}$

CD = $\sqrt{\frac{(8)^2 + (6)^2}{2}-(\frac{1}{2}(10))^2}$

CD = $\sqrt{\frac{(64 + 36)}{2}-(5)^2}$

CD = $\sqrt{\frac{100}{2}-25}$

CD = $\sqrt{50 - 25}$

CD = $\sqrt{25}$

CD = 25 cm

jadi, panjang garis berat CD = 5 cm

9. perhatikan gambar dibawah ini:

diketahui panjang PR = 13 cm, panjang QR = 15 cm, dan panjang PQ = 14 cm. tentukanlah panjang garis bagi RS pada $\triangle$PQR...?

penyelesaian:

Panjang PR = 13 cm

Panjang QR = 15 cm

Panjang PQ = 14 cm

Panjang garis bagi RS ..........?

RS  = $\sqrt{(PR)(QR) \left [ 1-\frac{(PQ)^2}{(PR+QR)^2} \right]}$

RS  = $\sqrt{(13)(15) \left [ 1-\frac{(14)^2}{(13+15)^2} \right]}$

RS  = $\sqrt{(195) \left [ 1-\frac{(14)(14)}{(28)(28)} \right]}$

RS  = $\sqrt{(195) \left [ 1-\frac{(1)(1)}{(2)(2)} \right]}$

RS  = $\sqrt{(195) \left [ 1-\frac{(1)}{(4)} \right]}$

RS  = $\sqrt{(195) \left [\frac{4 - 1}{4} \right]}$

RS  = $\sqrt{(195) \left [\frac{3}{4} \right]}$

RS  = $\sqrt{(3.65) \left [\frac{3}{4} \right]}$

RS  = $\frac{3}{2}$ $\sqrt{65}$

Jadi, panjang garis bagi RS = $\frac{3}{2}$ $\sqrt{65}$

10. perhatikan gambar dibawah ini:

diketahui ST // PQ, panjang RS = 12 cm, PS = 4 cm, dan RT = 27 cm, hitunglah panjang QT.............?penyelesaian:

RS = 12 cm

PS = 4 cm

RT = 27 cm

PR = 4 + 12 = 16 cm

QT = x

QR = 27 + x

$\frac{PR}{PS}$ = $\frac{QR}{QT}$

$\frac{16}{4}$ = $\frac{27 + x}{x}$

4 = $\frac{27 + x}{x}$

4x = 27 + x

4x - x = 27

3x = 27

x = $\frac{27}{3}$ 

x = 9 cm

11. Perhatikan gambar di bawah ini!

gambar $\triangle$ABC merupakan segitiga siku-siku. panjang AB = 5 cm, panjang AC = 12 cm, Panjang BC = 13 cm. dan panjang AM = panjang CM. tentukanlah titik berat dengan nilai BO dan OM pada $\triangle$ABC...?

jawaban:

Ingat kembali cara menentukan panjang garis berat pada segitiga siku-siku:

AB = 5 

AC = 12 cm

BC = 13 cm

untuk menentukan titik berat nilai BO dan OM terlebih dahulu tentukan panjang garis berat BM ....?

BM = $\sqrt{\frac{(BC)^2 + (AB)^2}{2}-(\frac{1}{2}AC)^2}$

BM = $\sqrt{\frac{(13)^2 + (5)^2}{2}-(\frac{1}{2}12)^2}$

BM = $\sqrt{\frac{(169 + 25)}{2}- 6^2}$

BM = $\sqrt{\frac{(194)}{2}- 6^2}$

BM = $\sqrt{97 -  36}$

BM = $\sqrt{61}$

maka titik berat nilai BO dan OM pada gambar diatas:

dimana panjang garis berat BM = BO + OM

OM = $\frac{1}{3}$BM

OM = $\frac{1}{3}$$\sqrt{61}$

BO = $\frac{2}{3}$BM

BO = $\frac{2}{3}$$\sqrt{61}$

jadi, nilai BO = $\frac{2}{3}$$\sqrt{61}$ dan OM = $\frac{1}{3}$$\sqrt{61}$

12. Perhatikan gambar dibawah ini!

diketahui segitiga siku-siku. panjang PQ = 12 cm, panjang PR = 5 cm, dan panjang QR = 13 cm. tentukanlah besar sudut Q dan sudut R dengan menggunakan aturan rumus Tangen...?

jawaban:

PQ = x = 12 cm

PR = y = 5 cm

QR = r = 13 cm

tan $x^0$ = $\frac{y}{x}$

tan $x^0$ = $\frac{5}{12}$

$x^0$ = $tan^{-1}$ $\frac{5}{12}$

$x^0$ = $tan^{-1}$ (0,42)

$x^0$ = $22,78^0$ 

$\angle$Q =  $22,78^0$ 

maka sudut R

$\angle$R = $180^0$ - ($\angle$P + $\angle$Q)

$\angle$R = $180^0$ - ($90^0$ + $22,78^0$)

$\angle$R = $180^0$ - $112,78^0$

$\angle$R = $67,22^0$

jadi, $\angle$Q =  $22,78^0$ dan $\angle$R = $67,22^0$

13. Seorang nakhoda kapal melihat puncak mercusuar yang berjarak 45 meter dari kapal. Jika diketahui tinggi mercusuar 60 meter, tentukan jarak nakhoda dari puncak mercusuar tersebut!

a. 75 meter

b. 80 meter

c. 90 meter

d. 62 meter

e. 17 meter

penyelesaian:

ilustrasi gambar:

maka jarak nakhoda dari puncak mercusuar dengan menggunakan rumus Teorema Pythagoras:

keterangan:

AB = 45 m

AC= jarak nakhoda dari puncak mercusuar

BC = 60 m

$AB^{2}$ + $BC^{2}$ = $AC^{2}$

$45^{2}$ + $60^{2}$ = $AC^{2}$

2025 + 3600= $AC^{2}$

5625 = $AC^{2}$

$AC^{2}$ = 5625

AC = $\sqrt{5625}$

AC = 75 m

Jadi, jarak nakhoda dari puncak mercusuar  = 75 m

14. perhatikan gambar dibawah ini:

gambar diatas merupakan segitiga sembarang jika diketahui sudut B = $100^{0}$, sudut C = $25^{0}$. dan panjang BC = 38 cm, tentukanlah panjang AC...?

Penyelesaian:

sudut B = $100^{0}$

sudut C = $25^{0}$

BC = 38 cm

AC = .....?

tentukanlah sudut A

$\angle$A = $180^{0}$ - ($\angle$B + $\angle$C)

$\angle$A = $180^{0}$ - ($100^{0}$ + $25^{0}$)

$\angle$A = $180^{0}$ - $125^{0}$

$\angle$A = $55^{0}$ 

tentukanlah panjang sisi AC..?

$\frac{BC}{Sin A^0}$ = $\frac{AC}{Sin B^0}$

$\frac{38}{Sin 55^0}$ = $\frac{AC}{Sin 100^0}$

$\frac{38}{0,819}$ = $\frac{AC}{0,985}$  

AC = 0,985 x $\frac{38}{0,819}$ 

AC = 0,985 x 46,398

AC = 45,702

Jadi panjang AC = 45,702

15. sudut elevasi puncak tiang bendera dari tempat yang jaraknya 400 meter dari kaki tiang adalah $45^0$. tentukan tinggi tiang...?

a. 20 meter

b. 30 meter

c. 40 meter

d. 50 meter

e. 80 meter

penyelesaian:

ilustrasi gambar:

maka tinggi pohon mangga dapat dihitung dengan menggunakan rumus Teorema Pythagoras:

keterangan:

(tan $45^0$ = 1)

BC = x .....sisi yang mengapit sudut x

AB = y .....sisi didepan sudut x

BC = x = 400 meter

tan $x^0$  = $\frac{y}{x}$ 

1 = $\frac{y}{400}$ 

1 x 400 = y

y = 400

maka tinggi bendera itu adalah 400 meter

Saran dan Kritik tentang Kumpulan Soal Latihan Lengkap Segitiga

Demikianlah matari Cara Kumpulan Soal Latihan Lengkap pada Segitiga. materi segitiga merupakan macam-macam Bangun Datar. tentunya banyak kekurangan dan kelemahan penulis, penulis banyak berharap kepada para pembaca memberikan kritik saran yang membangun demi sempurnya artikel ini. terimakasih.

silahkan kunjungi artikel terkait materi Segitiga: