hello teman-teman materi kali ini kita akan membahas latihan soal mengenai
bagaimana cara menentukan Hubungan Sudut pusat dan Sudut Keliling Lingkaran, Rumus Sudut Pusat dan Sudut Keliling, Garis Singgung Persekutuan Luar Dua Lingkaran, Garis Singgung Persekutuan Dalam Dua Lingkaran, Menentukan Luas Lingkaran, Menentukan Keliling Lingkaran, Luas Juring Lingkaran, Menentukan Panjang Busur Lingkaran, Menentukan Panjang Apotema Lingkaran, Menentukan Panjang Tali Busur Lingkaran, Menentukan Panjang Jari-Jari dan Diameter jika hanya Panjang Busur
lingkaran yang diketahui, Menentukan Panjang Jari-Jari dan Diameter jika hanya keliling lingkaran
yang diketahui, Menentukan Panjang Jari-Jari dan Diameter jika hanya luas juring lingkaran
yang diketahui, Menentukan Panjang Jari-Jari dan Diameter jika hanya luas lingkaran yang
diketahui.
Kumpulan Materi Lingkaran:
Loading....
Latihan Soal Lengkap Kedua Lingkaran
1. Perhatikan gambar di samping !
AB adalah garis singgung persekutuan luar. Diketahui AM = 16 cm, BN= 7 cm dan MN = 41 cm. Panjang AB adalah
A. 13,5 cm
B. 27 cm
C. 32 cm
D. 40 cm
jawaban:
R = panjang AM = 16 cm
r = panjang BN = 7 cm
jarak titik pusat kedua lingkaran (panjang AB)
disimbolkan JT.
JT = MN = 41 cm
Sehingga GSL………..?
$GSL^{2}$ = $JT^{2}$ - $(R - r)^{2}$
$GSL^{2}$ = $41^{2}$ - $(16 - 7)^{2}$
$GSL^{2}$ = 1681 - 81
$GSL^{2}$ = 1600
GSL = $\sqrt{1600}$
GSL = 40
Jadi, garis singgung persekutuan luar dua lingkaran = 40 cm
2. Dua lingkaran masing-masing dengan jari-jari 17 cm dan 25 cm, panjang garis singgung persekutuan luarnya 15 cm. Jarak antara kedua pusat lingkaran tersebut adalah …
A. 12 cm
B. 17 cm
C. 23 cm
D. 35 cm
jawab:
Diketahui:
R = 25 cm
r = 17 cm
jarak titik pusat kedua lingkaran
disimbolkan JT.
JT = …….. cm
GSL = 15 cm
Sehingga JT………..?
$GSL^{2}$ = $JT^{2}$ - $(R - r)^{2}$
$15^{2}$ = $JT^{2}$ - $(25 - 17)^{2}$
225 = $JT^{2}$ - $(8)^{2}$
225 = $JT^{2}$ - 64
$JT^{2}$ = 225 + 64
$JT^{2}$ = 289
JT = $\sqrt{225}$
JT = 17
Jadi, jarak pusat kedua lingkaran = 17 cm
3. Diketahui dua buah lingkaran dengan pusat di A dan B, masing-masing berjari-jari 34 cm dan 10 cm. Garis CD merupakan garis singgung persekutuan luar. Bila garis CD = 32 cm, panjang AB adalah …
A. 66 cm
B. 44 cm
C. 42 cm
D. 40 cm
jawab:
Diketahui:
R = 34 cm
r = 10 cm
jarak titik pusat kedua lingkaran
disimbolkan JT.
JT = …….. cm
GSL = panjang CD = 32 cm
Sehingga JT………..?
$GSL^{2}$ = $JT^{2}$ - $(R - r)^{2}$
$32^{2}$ = $JT^{2}$ - $(34 - 10)^{2}$
1024 = $JT^{2}$ - $(24)^{2}$
1024 = $JT^{2}$ - 576
$JT^{2}$ = 1024 + 576
$JT^{2}$ = 1600
JT = $\sqrt{1600}$
JT = 40
Jadi, jarak pusat kedua lingkaran = panjang AB = 40 cm
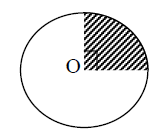
4. O adalah titik pusat lingkaran dengan keliling 220 cm. Luas juring yang diarsir … (π = $\frac{22}{7}$)
A. 3.850 $cm^{2}$
B. 1.925 $cm^{2}$
C. 962,5 $cm^{2}$
D. 880 $cm^{2}$
jawab:
K = keliling Lingkaran = 220 cm
r = jari-jari lingkaran
π = $\frac{22}{7}$
maka:
r = $\frac{220}{2.\frac{22}{7}}$
r = $\frac{220.7}{2. 22}$
r = $\frac{10.7}{2}$
r = 5 x 7
r = 35
sehingga:
Luas Juring Lingkaran
Keterangan:
π = $\frac{22}{7}$
r = 35
x= sudut pusat lingkaran = $90^{0}$
360 = satu putaran lingkaran
r = $\frac{1}{2}$d
Luas Juring Lingkaran = $\frac{x^0}{360^0}$π$r^{2}$
Luas Juring Lingkaran = $\frac{90^0}{360^0}$ x $\frac{22}{7}$ x $35^{2}$
Luas Juring Lingkaran = $\frac{1}{4}$ x $\frac{22}{7}$ x 35 x 35
Luas Juring Lingkaran = $\frac{1}{4}$ x 22 x 5 x 35
Luas Juring Lingkaran = $\frac{1}{2}$ x 11 x 5 x 35
Luas Juring Lingkaran = $\frac{1925}{2}$
Luas Juring Lingkaran = 962,5
sehingga luas juring lingkaran = 962,5 $cm^{2}$
5. Pada gambar di samping diketahui ∠ PSR = $37^{0}$. Besar sudut POR adalah …
A. $64^{0}$
B. $74^{0}$
C. $84^{0}$
D. $94^{0}$
penyelesaian:
sudut pusat lingkaran = ∠POR = .....?
sudut keliling lingkaran = ∠PSR = $37^{0}$
Sudut Pusat Lingkaran = 2 Sudut Keliling Lingkaran
Sudut Pusat Lingkaran = 2 x $37^{0}$
Sudut Pusat Lingkaran = $74^{0}$
6. Perhatikan gambar berikut! Panjang PQ = 20 cm, AB = 25 cm dan AP = 9 cm. Perbandingan luas lingkaran berpusat di A dengan luas
lingkaran berpusat di B adalah …
R = AP = 9 cm
r = QB = .... cm
jarak titik pusat kedua lingkaran (panjang AB) disimbolkan JT.
GSD = panjang PQ = 20 cm
JT = panjang AB = 25 cm
Sehingga GSD………..?
$GSD^{2}$ = $JT^{2}$ - $(9 + r)^{2}$
$20^{2}$ = $25^{2}$ - $(9 + r)^{2}$
$(9 + r)^{2}$ = $25^{2}$ - $20^{2}$
$(9 + r)^{2}$ = 625 - 400
$(9 + r)^{2}$ = 225
9 + r = $\sqrt{225}$
r = 15 - 9
r = 6
Jadi, panjang jari-jari kecil = 6
maka:
keterangan:
$r^{2}_1$ = 9
$r^{2}_2$ = 6
perbandingan luas lingkaran besar : luas lingkaran kecil = $\frac{π.r^{2}_1}{π.r^{2}_2}$
perbandingan luas lingkaran besar : luas lingkaran kecil = $\frac{9^{2}}{6^{2}}$
perbandingan luas lingkaran besar : luas lingkaran kecil = $\frac{9.9}{6.6}$
perbandingan luas lingkaran besar : luas lingkaran kecil = $\frac{3.3}{2.2}$
perbandingan luas lingkaran besar : luas lingkaran kecil = $\frac{9}{4}$
7. Gambar di atas menunjukkan daerah yang dibentuk oleh tali busur dalam lingkaran, 1 buah tali busur membentuk 2 daerah, 2 busur membentuk 4 daerah, 3 buah busur membentuk 6 daerah. Berapa yang dapat dibentuk bila dibuat 25 buah tali busur ?
A. 25
B. 35
C. 49
D. 50
jawab:
n= 2
bentuk model matematika
1 buah tali busur membentuk 2 daerah = 1 x n = 1 x 2 = 2
2 buah tali busur membentuk 4 daerah = 2 x n = 2 x 2 = 4
3 buah tali busur membentuk 4 daerah = 3 x n = 3 x 2 = 6
jika 25 buah tali busur maka berapa daerah yang terbentuk...?
25 buah tali busur membentuk ... daerah = 25 x n = 25 x 2 = 50
8. Gambar di atas menunjukkan daerah yang dibentuk oleh tali busur dalam lingkaran, 1 buah tali busur membentuk 2 daerah, 2 busur membentuk 4 daerah, 3 buah busur membentuk 6 daerah. Berapa yang dapat dibentuk bila dibuat 25 buah tali busur ?
A. 25
B. 35
C. 49
D. 50
jawab:
n= 2
bentuk model matematika
1 buah tali busur membentuk 2 daerah = 1 x n = 1 x 2 = 2
2 buah tali busur membentuk 4 daerah = 2 x n = 2 x 2 = 4
3 buah tali busur membentuk 4 daerah = 3 x n = 3 x 2 = 6
jika 25 buah tali busur maka berapa daerah yang terbentuk...?
25 buah tali busur membentuk ... daerah = 25 x n = 25 x 2 = 50
Panjang busur kecil PQ = 11 cm. Panjang jari-jari lingkaran adalah … (π = $\frac{22}{7}$)
A. 7 cm
B. 9 cm
C. 12 cm
D. 14 cm
jawab:
Menentukan Panjang Busur Lingkaran
Keterangan:
π = $\frac{22}{7}$
r = jari-jari lingkaran
x = $45^{0}$
360 = satu putaran lingkaran
PB = Panjang Busur PQ Lingkaran = 11
rumus menentukan Jari-jari lingkaran jika hanya Panjang Busur yang diketahui:
r = $\frac{360^0.PB}{2x^0.π}$
r = $\frac{360^0.11}{2.45^0.\frac{22}{7}}$
r = $\frac{8.11}{2.\frac{22}{7}}$
r = $\frac{8.11.7}{44}$
r = $\frac{88.7}{44}$
r = 2 x 7
r = 14
sehingga panjang jari-jari lingkaran = 14 cm
9. diketahui jari-jari lingkaran = 14 cm. dan sudut pusat lingkaran = $90^{0}$ derajat. tentukanlah Luas tembereng yang diarsir adalah …
a. $70^{0}$
b. $80^{0}$
c. $90^{0}$
c. $95^{0}$
jawab:
untuk menentukan luas tembereng lingkaran ada beberapa langkah:
langkah pertama tentukanlah luas juring lingkaran
π = $\frac{22}{7}$
r = 14 cm
x= sudut pusat lingkaran = $90^{0}$
360 = satu putaran lingkaran
Luas Juring Lingkaran = $\frac{x^0}{360^0}$π$r^{2}$
Luas Juring Lingkaran = $\frac{90^0}{360^0}$ x $\frac{22}{7}$ x $14^{2}$
Luas Juring Lingkaran = $\frac{1}{4}$ x $\frac{22}{7}$ x 14 x 14
Luas Juring Lingkaran = $\frac{1}{4}$ x 22 x 2 x 14
Luas Juring Lingkaran = $\frac{1}{4}$ x (44 x 14)
Luas Juring Lingkaran = 11 x 14
Luas Juring Lingkaran = 154
Luas Juring Lingkaran = 154 $cm^{2}$
langkah kedua tentukanlah luas segitiga:
keterangan:
$x^{0}$ = $90^{0}$
AO = 14 cm
BO = 14 cm
luas segitiga AOC = $\frac{1}{2}$ x (AO x BO) Sin $x^{0}$
luas segitiga AOC = $\frac{1}{2}$ x (14 x 14) Sin $90^{0}$
luas segitiga AOC = 7 x 14 x 1
luas segitiga AOC = 7 x 14 x 1
luas segitiga AOC = 98
luas segitiga AOC = 98 $cm^{2}$
jadi
luas tembereng lingkaran = luas juring lingkaran AOB - luas segitiga AOB
luas tembereng lingkaran = 154 $cm^{2}$ - 98 $cm^{2}$
luas tembereng lingkaran = 154 $cm^{2}$ - 98 $cm^{2}$
luas tembereng lingkaran = 56 $cm^{2}$
10. Perhatikan gambar berikut ini!
Luas juring daerah yang diarsir adalah …
A. 251,4 $cm^{2}$
B. 125,6 $cm^{2}$
C. 50,24 $cm^{2}$
D. 25,12 $cm^{2}$
jawab:
langkah pertama tentukanlah luas juring lingkaran
π = $\frac{22}{7}$
r = 20 cm
x= sudut pusat lingkaran = $72^{0}$
360 = satu putaran lingkaran
Luas Juring Lingkaran = $\frac{x^0}{360^0}$π$r^{2}$
Luas Juring Lingkaran = $\frac{72^0}{360^0}$ x $\frac{22}{7}$ x $20^{2}$
Luas Juring Lingkaran = $\frac{1}{5}$ x $\frac{22}{7}$ x 20 x 20
Luas Juring Lingkaran = $\frac{22}{7}$ x 4 x 20
Luas Juring Lingkaran = $\frac{22}{7}$ x (80)
Luas Juring Lingkaran = $\frac{1760}{7}$
Luas Juring Lingkaran = 251,4
Luas Juring Lingkaran = 251,4 $cm^{2}$
11. Dua lingkaran A dan B masing-masing berdiameter 26 cm dan 16 cm. Jika jarak AB = 26 cm, panjang garis singgung persekutuan luar kedua lingkaran tersebut adalah …
A. 22 cm
B. 24 cm
C. 26 cm
D. 28 cm
jawaban:
diameter A = 26 cm
diameter B = 16 cm
R = $\frac{1}{2}$d = $\frac{1}{2}$ 26 cm = 13 cm
r = $\frac{1}{2}$d = $\frac{1}{2}$ 16 cm = 8 cm
jarak titik pusat kedua lingkaran AB
disimbolkan JT.
JT = AB = 26 cm
Sehingga GSL………..?
$GSL^{2}$ = $JT^{2}$ - $(R - r)^{2}$
$GSL^{2}$ = $26^{2}$ - $(13 - 8)^{2}$
$GSL^{2}$ = 676- 25
$GSL^{2}$ = 651
GSL = $\sqrt{651}$
GSL = 25,5
Jadi, garis singgung persekutuan luar dua lingkaran = 25,5 cm
12. Perhatikan gambar lingkaran di bawah ini!
Jika O pusat lingkaran, dan panjang OP = 21 cm, maka panjang busur kecil PQ adalah … (π = $\frac{22}{7}$)
a. 132 cm
b. 66 cm
c. 22 cm
d. 12 cm
Jawaban:
Keterangan:
π = $\frac{22}{7}$
r = jari-jari lingkaran = OP = 21 cm
x = sudut pusat lingkaran = $60^{0}$
satu putaran lingkaran = 360 derajat
Panjang Busur Lingkaran = $\frac{x^0}{360^0}$2πr
Panjang Busur Lingkaran = $\frac{60^0}{360^0}$ x 2 x $\frac{22}{7}$ x 21
Panjang Busur Lingkaran = $\frac{1}{6}$ x 2 x $\frac{22}{7}$ x 21
Panjang Busur Lingkaran = $\frac{1}{3}$ x 22 x 3
Panjang Busur Lingkaran = 22
jadi, panjang busur lingkaran = 22 cm
13. Panjang garis singgung persekutuan dalam dua lingkaran 8 cm. Jika jarak titik pusat kedua lingkaran 17 cm dan panjang jari-jari salah satu lingkaran 10 cm, maka panjang jari-jari lingkaran yang lain adalah …
a. 5 cm
b. 6 cm
c. 7 cm
d. 9 cm
R = 10 cm
r = .... cm
jarak titik pusat kedua lingkaran disimbolkan JT.
JT = 17
GSD = 8 cm
Sehingga
$GSD^{2}$ = $JT^{2}$ - $(R + r)^{2}$
$8^{2}$ = $17^{2}$ - $(10 + r)^{2}$
64 = 289 - $(10 + r)^{2}$
$(10 + r)^{2}$ = 289 - 64
$(10 + r)^{2}$ = 225
10 + r = $\sqrt{225}$
r = 15 - 10
r = 5
Jadi, panjang jari-jari lingkaran lain = 5 cm
14. Diketahui dua buah lingkaran dengan pusat A dan B, dengan panjang jari-jari masing-masing 7 cm dan 2 cm. Jika jarak AB = 13 cm, maka panjang garis singgung persekutuan luar kedua lingkaran tersebut adalah ...
A. 5 cm
B. 6 cm
C. 12 cm
D. 15 cm
jawab:
R = 7 cm
r = 2 cm
jarak titik pusat kedua lingkaran (panjang AB)
disimbolkan JT.
JT = AB = 13 cm
Sehingga GSL………..?
$GSL^{2}$ = $JT^{2}$ - $(R - r)^{2}$
$GSL^{2}$ = $13^{2}$ - $(7 - 2)^{2}$
$GSL^{2}$ = 169 - 25
$GSL^{2}$ = 144
GSL = $\sqrt{144}$
GSL = 12
Jadi, garis singgung persekutuan luar dua lingkaran = 12 cm
Saran dan Kritik
Demikianlah matari mengenai Latihan Soal Lengkap Pertama lingkaran. materi
lingkaran merupakan unsur-unsur bangun datar. tentunya banyak
kekurangan dan kelemahan penulis, penulis banyak berharap kepada para
pembaca memberikan kritik saran yang membangun demi sempurnya artikel ini.
terimakasih.
segitiga
lingkaran
bangun datar
bangun ruang




Post a Comment for "Kumpulan Latihan Soal Lengkap Lingkaran "