BAGAIMANA MENGHITUNG PANJANG BUSUR DAN APOTEMA LINGKARAN

» Menghitung Panjang Busur Lingkaran

Hello teman-teman, materi kali ini kita akan membahas bagaimana cara menentukan Panjang Busur Lingkaran, dan Apotema Lingkaran, Dimana materi sebelumnya kita sudah membahas pengertian Lingkaran dan unsur-unsurnya. Nah materi kali ini Kita akan membahas bagaimana cara cara menentukan Panjang Busur Lingkaran, Apotema Lingkaran.

∩AB simbol ini dibaca panjang busur AB sebagaimana ilustrasi gambar diatas. 

rumus menentukan panjang busur lingkaran:

Atau dengan rumus:

Langkah-Langkah menentukan panjang busur lingkaran:

Langkah I : tentukan besar sudut lingkaran atau sudut teta

Langkah II : tentukan jari-jari lingkaran atau diameter lingkaran

Langkah III: sudut penuh lingkaran = 360⁰

Untuk menentukan panjang busur lingkaran ada hubungannya dengan menentukan keliling lingkaran. Karena Panjang busur lingkaran merupakan bagian dari keliling lingkaran itu sendiri.

contoh:

perhatikan gambar dibawah ini:

Jari-jari lingkaran diatas adalah 14 cm. tentukan panjang busur lingkaran AB.

Jawaban:

Sudut pusat lingkaran = 45⁰

r = 14 cm

π = 22/7

1 kali putaran lingkaran = 360⁰

Panjang Busur AB…??

Panjang Busur AB =(sudut pusat lingkaran/360⁰)*keliling lingkaran

Panjang Busur AB =(sudut pusat lingkaran/360⁰)*2πr

Panjang Busur AB =(45⁰/360⁰)*2*(22/7)*(14)

Panjang Busur AB =(1/8)*2*(22)*(2)

Panjang Busur AB =(22/8)*2*2

Panjang Busur AB =(22/8)*4

Panjang Busur AB =(22/8)*4

Panjang Busur AB =(88/8)

Panjang Busur AB = 11 cm

» Menghitung Apotema Lingkaran

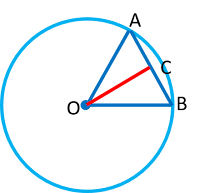
perhatikan gambar di bawah ini:

Sebelumnya kita sudah mempelajari tentang pengertian lingkaran beserta unsur-unsurnya. Apotema lingkaran merupakan salah satu bagian dari unsur-unsur lingkaran. Digambar diatas apotema lingkaran adalah garis OC. Nah untuk menentukan apotema lingkaran tidak terlepas dari teorema Pythagoras segitiga dan teorema jumlah trigonometri cosinus.

contoh:

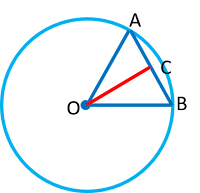
perhatikan gambar dibawah ini:

jari-jari lingkaran pada gambar diatas adalah 5 cm. besar sudut ∆AOB = 60⁰. tentukanlah apotema lingkaran pada gambar di atas!

jawaban:

Langkah-Langkah Menentukan Apotema Lingkaran:

langkah 1:kita tentukan panjang sisi AB   dengan menggunakan rumus penjumlahan trigonometri cosinus.

Diketahui sudut O = 60⁰.

Jari-jari lingkaran = 5 cm

OA = AB = jari-jari lingkaran, sehingga,

OA = 5

OB = 5

AB² = OA² + OB² – 2(OA)(OB) cos ʘ

AB² = 5² + 5² – 2(5)(5) cos 60

AB² = 25 + 25 – 2(25) (1/2)

AB² = 50 – 25

AB² = 25

AB = √25

AB = 5

langkah 2: kita tentukan panjang OC atau Apotema Lingkaran dengan menggunakan rumus teorema pythagoras:

Tinggi OC merupakan apotema lingkaran. Untuk menentukan panjang OC digunakan rumus teorema pythagoras.

OC² = OA² – OB²

OC² = 5² – (5/2)²

OC² = 25 – (25/4)

OC² = (100/4) – (25/4)

OC² = ($\frac{75}{4}$)

OC² = √75/4

OC = $\frac{5}{2}$(√3)

Soal-Soal Latihan Menghitung Panjang Busur dan Apotema Lingkaran

1. pada gambar dibawah ini: Jari-jari lingkaran diatas adalah 28 cm. panjang busur lingkaran AB………….?
a. 22 cm b. 23 cm c. 34 cm	d. 44 cm e. 45 cm
Kunci Jawaban: d. x = 900 r = 28 π = $\frac{22}{7}$ Panjang Busur AB = ……? Panjang Busur AB = ($\frac{x}{360}$) x 2πr Panjang Busur AB = ($\frac{90}{360}$) x 2 x ($\frac{22}{7}$)(28) Panjang Busur AB = ($\frac{1}{4}$) x 2 x 22 x 4 Panjang Busur AB = 2 x 22 Panjang Busur AB = 44   Panjang Busur AB = 44 cm

2. pada gambar dibawah ini: Jari-jari lingkaran diatas adalah 28 cm. panjang busur lingkaran AB………….?
a. 22 cm b. 44 cm c. 33  cm	d. 45 cm e. 11 cm
Kunci Jawaban: b. x = 1800 d = 28 cm r = $\frac{1}{2}$28 = 14 cm π = $\frac{22}{7}$ Panjang Busur AB = ……? Panjang Busur AB = ($\frac{x}{360}$) x 2πr Panjang Busur AB = ($\frac{180}{360}$) x 2($\frac{22}{7}$)(14) Panjang Busur AB = ($\frac{1}{2}$) x 2 x 22 x 2 Panjang Busur AB = 2 x 22 Panjang Busur AB = 44 Panjang Busur AB = 44 cm

3. pada gambar dibawah ini: Jari-jari lingkaran diatas adalah 56 cm dan sudut pusat lingkaran 2700. tentukan panjang busur lingkaran AB………….?
a. 255 cm b. 256 cm c. 254 cm	d. 246 cm e. 264 cm
Kunci Jawaban: e. x = 2700 r = 56 cm π = $\frac{22}{7}$ Panjang Busur AB = ……? Panjang Busur AB = ($\frac{x}{360}$) x 2πr Panjang Busur AB = ($\frac{270}{360}$) x 2 x ($\frac{22}{7}$)(56) Panjang Busur AB = ($\frac{3}{4}$) x 2 x 22 x 8 Panjang Busur AB = 3 x 2 x 22 x 2 Panjang Busur AB = 3 x 88 Panjang Busur AB = 264 cm

4. pada gambar dibawah ini: Jari-jari lingkaran pada gambar diatas adalah 10 cm. besar sudut ∆AOB = 600.  Tentukanlah apotema ………….?
a. 208 cm2 b. 408 cm2 c. 308  cm2	d. 108 cm2 e. 306 cm2
Kunci Jawaban: c. x = 600 r = 10 cm OA = AB = jari-jari lingkaran, sehingga: OA = 10 OB = 10 Menggunakan rumus teorema Pythagoras. AB2 = OA2 + OB2 – 2 (OA) (OB) cos x AB2 = 102 + 102 – 2 (10) (10) cos 60 AB2 = 100 + 100 – 2 (10) (10) $\frac{1}{2}$ AB2 = 200 – 100 AB2 = 100 AB = √100 AB = 10 Tinggi OC merupakan Apotema lingkaran. Untuk menentukan panjang OC digunakan rumus teorema Pythagoras OC2 = OA2 – OB2 OC2 = 102 – 52 OC2 = 100 – 25 OC2 = 75 OC = √75 OC = 5√3

5. pada gambar dibawah ini: Jari-jari lingkaran pada gambar diatas adalah 20 cm. besar sudut ∆AOB = 600.  Tentukanlah apotema ………….?
a. 208 cm2 b. 408 cm2 c. 308  cm2	d. 108 cm2 e. 306 cm2
Kunci Jawaban: c. x = 600 r = 20 cm OA = AB = jari-jari lingkaran, sehingga: OA = 20 OB = 20 Menggunakan rumus teorema Pythagoras. AB2 = OA2 + OB2 – 2 (OA) (OB) cos x AB2 = 202 + 202 – 2 (20) (20) cos 60 AB2 = 400 + 400 – 2 (20) (20) $\frac{1}{2}$ AB2 = 800 – 400 AB2 = 400 AB = √400 AB = 20 Tinggi OC merupakan Apotema lingkaran. Untuk menentukan panjang OC digunakan rumus teorema Pythagoras OC2 = OA2 – OB2 OC2 = 202 – 102 OC2 = 400 – 100 OC2 = 300 OC = √300 OC = 10√3

Referensi Panjang Busur Dan Apotema Lingkaran:

Soal-Soal UN Matematika SMP. 

Demikianlah matari mengenai Panjang Busur Dan Apotema Lingkaran. Panjang Busur Dan Apotema Lingkaran merupakan materi tentang bangun datar lingkaran. tentunya banyak kekurangan dan kelemahan penulis, penulis banyak berharap kepada para pembaca memberikan kritik saran yang membangun demi sempurnya artikel ini. terimakasih.

silahkan kunjungi artikel terkait tentang Lingkaran: 

Next 1: