Garis Singgung Persekutuan Luar Dua Lingkaran : (Pengertian, Menentukan Panjang, Panjang Salah Satu Jari-jari Lingkaran Kecil & Besar, dan Jarak Titik Pusat)

◊ Pengertian Garis Singgung Persekutuan Luar Dua Lingkaran

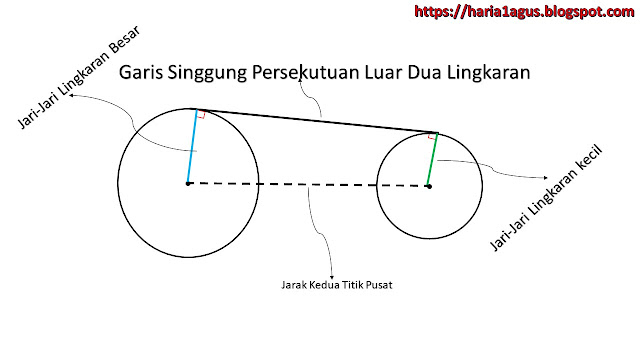
Pembahasan Kali ini Mengenai Garis Singgung Persekutuan Luar dua lingkaran. Garis Singgung Persekutuan Luar Dua Lingkaran terdapat dua buah lingkaran yang besar jari-jarinya berbeda. garis singgung yang menghubungkan dua buah lingkaran tidak berpotongan terhadap jarak titik pusat kedua lingkaran. biar jelas perhatikan gambar dibawah ini:

Rumus Garis Singgung Persekutuan Luar Dua Lingkaran:

GSL² = JT² – (R - r)²

Keterangan (cara baca):

GSL = Garis singgung persekutuan Luar Dua Lingkaran

JT = jarak titik pusat  kedua lingkaran

R = Lingkaran Besar

r = lingkaran kecil

◊ Menentukan Panjang Garis Singgung Persekutuan Luar Dua Lingkaran

Contoh:

perhatikan gambar dibawah ini:

diketahui panjang AB = 25 cm. tentukanlah Panjang Garis Singgung Luar Dua Lingkaran..?

jawaban:

Penyelesaian:

Diketahui: R = 15 cm r = 8 cm jarak titik pusat kedua lingkaran (panjang AB) disimbolkan JT. JT = 25 Sehingga GSL………..? GSL2 = JT2 – (R - r)2 GSL2 = 252 – (15 - 8)2 GSL2 = 625 – (7)2 GSL2 = 625 – 49 GSL2 = 576 GSL = √576 GSL = 24

◊ Panjang Salah Satu Jari-Jari Lingkaran Kecil pada  Garis Singgung Persekutuan Luar Dua Lingkaran

contoh:

Perhatikan gambar dibawah ini:

Diketahui: Panjang garis singgung luar dua lingkaran = √285 cm. panjang AB = 17 cm. tentukanlah jari-jari lingkaran B..?

Penyelesaian:

Diketahui: R = 5 cm r = ………. cm jarak titik pusat kedua lingkaran (panjang AB) disimbolkan JT. JT = 17 cm GSL = √285 cm Sehingga GSL………..? GSL2 = JT2 – (R - r)2 (√285)2 = 172 – (5 - r)2 285 = 289– (5 - r)2 (5 - r)2 =289 – 285 (5 - r)2 = 4 (5 - r) = √4 5 - r  = 2 - r = 2 - 5 - r = -3 r = 3 jadi, jari-jari kecil = 3 cm

◊ Panjang Salah Satu Jari-Jari Lingkaran Besar pada  Garis Singgung Persekutuan Luar Dua Lingkaran

contoh:

perhatikan gambar dibawah ini:

Diketahui: Panjang garis singgung luar dua lingkaran = 48 cm,panjang AB = 52 cm. dan jari-jari B = 12 cm. tentukanlah jari-jari lingkaran A..?

penyelesaian:

Penyelesaian:

Diketahui: R = …. cm r = 12 cm jarak titik pusat kedua lingkaran (panjang AB) disimbolkan JT. JT = 52 cm GSL = 48 cm Sehingga GSL………..? GSL2 = JT2 – (R - r)2 482 = 522 – (R - 12)2 2304 = 2704 – (R – 12)2 (R – 12)2 =2704 – 2304 (R – 12)2 = 400 (R – 12) = √400 R – 12 = 20 R = 20 + 12 R = 32 R = 32

◊ Jarak Titik Pusat pada  Garis Singgung Persekutuan Luar Dua Lingkaran

contoh:

perhatikan gambar dibawah ini:

tentukanlah panjang AB pada garis singgung luar dua lingkaran diatas?

penyelesaian:

Penyelesaian:

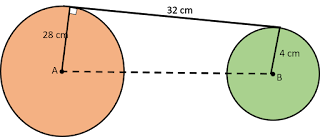
Diketahui: R =28 cm r = 4 cm jarak titik pusat kedua lingkaran (panjang AB) disimbolkan JT. JT = …….. cm GSL = 32 cm Sehingga JT………..? GSL2 = JT2 – (28 - 4)2 322 = JT2 – (24)2 1024 = JT2 – 576 JT2 – 576 =1024 JT2 = 1024 + 576 JT2 = 1600 JT = √1600 JT = 40 Jadi, Panjang AB = 40 cm

NO	MATERI LENGKAP LINGKARAN
1	Pengertian Lingkaran dan Unsur-Unsurnya
2	Menghitung Luas Lingkaran
3	Menghitung Luas Juring Lingkaran
4	Menghitung Keliling Lingkaran
5	Menghitung Panjang Busur dan Apotema Lingkaran
6	Menghitung Luas Tembereng Lingkaran
7	Garis Singgung Persekutuan dalam Dua Lingkaran
8	Garis Singgung Persekutuan luar Dua lingkaran
9	Hubungan Sudut dan Keliling Lingkaran

Referensi Soal Garis Singgung Persekutuan Luar Dua Lingkaran:

Soal-Soal UN Matematika SMP. 

Demikianlah matari mengenai Garis Singgung Persekutuan Luar Dua Lingkaran yaitu : Menentukan Panjang Garis Singgung Persekutuan Luar Dua Lingkaran, Panjang Salah Satu Jari-jari Lingkaran Kecil & Besar Garis Singgung Persekutuan Luar Dua Lingkaran, dan Jarak Titik Pusat Garis Singgung Persekutuan Luar Dua Lingkaran. Referensi Soal Garis Singgung Persekutuan Luar Dua Lingkaran merupakan materi tentang Bangun Datar lingkaran. tentunya banyak kekurangan dan kelemahan penulis, penulis banyak berharap kepada para pembaca memberikan kritik saran yang membangun demi sempurnya artikel ini. terimakasih.

silahkan kunjungi artikel terkait tentang Garis Singgung Lingkaran :