Metode Sarrus Matriks

Hello adek-adek kembali lagi kita membahas mengenai Metode Sarrus Matriks serta rumusnya. sebelumnya kita sudah belajar belajar tentang invers matriks. Konsep yang akan adek-adek pelajari pada artikel ini merupakan dasar untuk mempelajari materi selanjutnya untuk lebih jelasnya silahkan baca artikel ini sampai selesai.

Pengertian Metode Sarrus

Kita telah mempelajari bagaimana menentukan determinan matriks persegi ordo 2 dan sekarang akan dibahas determinan matriks persegi ordo 3.

Metode sarrus atau juga sering orang menyebutnya metode anyaman (Basketweave Method) adalah jalan alternatif dalam menghitung determinan dari matriks ordo 3 x 3.

Untuk menentukan determinan matriks ordo 3 × 3, dapat dilakukan dengan meletakkan lagi elemen-elemen kolom pertama dan kedua di belakang kolom ketiga kemudian dioperasikan sebagai berikut.

Menentukan Rumus Metode Sarrus

Rumus Menentukan Determinan Matriks

"det A = = a₁₁a₂₂a₃₃ + a₁₂ a₂₃a₃₁ + a₁₃a₂₁a₃₂ – a₁₃a₂₂a₃₁ – a₁₁a₂₃ a₃₂ – a₁₂ a₂₁a₃₃"

Langkah-Langkah Menentukan Rumus Metode Sarrus yaitu:

Untuk mencari determinan dari matriks persegi berordo 3 × 3, akan digunakan suatu metode yang dinamakan metode Sarrus. Adapun langkahlangkah yang harus Anda lakukan untuk mencari determinan matriks berordo 3 × 3 dengan metode Sarrus adalah sebagai berikut:

• Salin kembali kolom pertama dan kolom kedua matriks A di sebelahkanan tanda determinan.
• Hitunglah jumlah hasil kali elemen-elemen pada diagonal utama dan diagonal lain yang sejajar dengan diagonal utama (lihat gambar). Nyatakan jumlah hasil kali tersebut dengan Du
• 

• Hitunglah jumlah hasil kali elemen-elemen pada diagonal sekunder dan diagonal lain yang sejajar dengan diagonal sekunder (lihar gambar). Nyatakan jumlah hasil harga tersebut dengan Ds
• 
• Sesuai dengan defi nisi determinan matriks maka determinan dari matriks A adalah selisih antara Du dan Ds yaitu Du – Ds.
• 

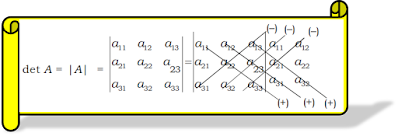
Pembahasan Metode Sarrus

Contoh Soal 1:

diketahui Matriks A = ${\begin{bmatrix} 3&4 &1\\ 2&-2&5 \\ 3&2&2 \\\end{bmatrix}}$ tentukan determinan matriks A....?

a. 11

b. 12

c. 13

d. 14

e. 15

penyelesaian:

A = ${\begin{bmatrix} 3&4 &1\\ 2&-2&5 \\ 3&2&2 \\\end{bmatrix}}$

$\left| A\right|$ = $\begin{vmatrix} 3&4 &1\\ 2&-2&5 \\ 3&2&2  \\\end{vmatrix}$ $\begin{matrix} 3&  4\\ 2&  -2\\ 3&  2\\\end{matrix}$

$\left| A\right|$ = 3.-2.2+ 4.5.3 + 1.2.2 - (1.-2.3 + 3.5.2 + 4.2.2)

$\left| A\right|$ = -12 + 60 + 4 - (-6 + 30 + 16)

$\left| A\right|$ = 52 - 40

$\left| A\right|$ = 12

soal 2

diketahui Matriks A = ${\begin{bmatrix} -3&4 &2\\ 2&1&3 \\ 1&0&-1 \\\end{bmatrix}}$ tentukan determinan matriks A....?

a. 12

b. 15

c. 17

d. 18

e. 21

penyelesaian:

A = ${\begin{bmatrix} -3&4 &2\\ 2&1&3 \\ 1&0&-1 \\\end{bmatrix}}$

$\left| A\right|$ = $\begin{vmatrix} -3&4 &2\\ 2&1&3 \\ 1&0&-1 \\\end{vmatrix}$ $\begin{matrix} -3&  4\\ 2&  1\\ 1&  0\\\end{matrix}$

$\left| A\right|$ = (-3.1.-1+ 4.3.1 + 2.2.0) - (1.1.2+ 0.3.-3 + (-1).2.4)

$\left| A\right|$ = (3+ 12 + 0) - (2+0-8)

$\left| A\right|$ = 15 - (-6)

$\left| A\right|$ = 15 + 16

$\left| A\right|$ = 21

soal 3

diketahui Matriks A = ${\begin{bmatrix} -5&3 &-2\\ 4&1&-1 \\ 2&0&3 \\\end{bmatrix}}$ tentukan determinan matriks A....?

a. -12

b. -15

c. -67

d. -58

e. -21

penyelesaian:

A = ${\begin{bmatrix} -5&3 &-2\\ 4&1&-1 \\ 2&0&3 \\\end{bmatrix}}$

$\left| A\right|$ = $\begin{vmatrix} -5&3 &-2\\ 4&1&-1 \\ 2&0&3 \\\end{vmatrix}$ $\begin{matrix} -5&  3\\ 4&  1\\ 2&  0\\\end{matrix}$

$\left| A\right|$ = (-5.1.3+ 3.-1.2 + -2.4.0) - (2.1.-2+ 0.-1.-5 + 3.4.3)

$\left| A\right|$ = (-15 -6 + 0) - (-4 + 5 + 36)

$\left| A\right|$ = -21 - 37

$\left| A\right|$ = -58