Penerapan Matriks Pada Sistem Persemaan Linear Dua Variabel
Hello adek-adek kembali lagi kita membahas mengenai Penerapan Matriks Pada Sistem Persemaan Linear Dua Variabel. sebelumnya kita sudah belajar belajar tentang invers matriks dan determinan matriks. Konsep yang akan adek-adek pelajari pada artikel ini merupakan dasar untuk mempelajari materi selanjutnya untuk lebih jelasnya silahkan baca artikel ini sampai selesai.
Pengertian Penerapan Matriks Pada Sistim Persemaan Linear Dua Variabel
Penerapan matriks dalam kehidupan sehari-hari sangatlah luas, baik di bidang ekonomi, ilmu-ilmu sosial, maupun ilmuilmu alam. Dengan menggunakan matriks, penyelesaian sistem persamaan linear menjadi lebih mudah, khususnya untuk sistem persamaan linear dengan dua variabel.
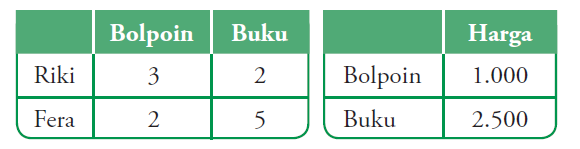
Riki dan Fera membeli alat tulis di koperasi sekolah. Riki membeli 3 buah bolpoin dan 2 buku, sedangkan Fera membeli 2 buah bolpoin dan 5 buku. Jika harga sebuah bolpoin Rp1.000,00 dan harga sebuah buku Rp2.500,00, berapakah harga belanjaan yang harus dibayar oleh masing-masing
siswa tersebut? Permasalahan tersebut dapat disajikan dalam bentuk tabel berikut.
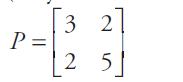
Menentukan Himpunan Penyelesaian Sistem Persamaan Linear Dua Variabel Metode Matriks
${\begin{bmatrix} a&b\\ c&d \end{bmatrix}}$ = $\begin{bmatrix} p \\ q \end{bmatrix}$
Cara I
ax + by = p ........................... (1)
cx + dy = q ........................... (2)
Ubahlah sistem persamaan ke bentuk persamaan matriks.
${\begin{bmatrix} a&b\\ c&d \end{bmatrix}}$ = $\begin{bmatrix} p \\ q \end{bmatrix}$
maka untuk menentukan nilai x dan y dengan rumus Metode Determinan Matriks:
nilai x = $\frac{{\begin{bmatrix} p&b\\ q&d \end{bmatrix}}}{{\begin{bmatrix} a&b\\ c&d \end{bmatrix}}}$
nilai y = $\frac{{\begin{bmatrix} a&p\\ c&q \end{bmatrix}}}{{\begin{bmatrix} a&b\\ c&d \end{bmatrix}}}$
Cara II
ax + by = p ........................... (1)
cx + dy = q ........................... (2)
Ubahlah sistem persamaan ke bentuk persamaan matriks.
${\begin{bmatrix} a&b\\ c&d \end{bmatrix}}$ = $\begin{bmatrix} p \\ q \end{bmatrix}$
maka untuk menentukan nilai x dan y dengan rumus Metode Invers Matriks:

Pembahasan Soal
Contoh Soal 1:
Imas dan Dewi pergi belanja ke pasar. Imas membeli 3 kg kentang dan 2 kg wortel, untuk itu Imas harus membayar Rp13.500,00. Adapun Dewi membeli 2 kg kentang dan 1 kg wortel. Dewi diharuskan membayar Rp8.500,00. Misalkan harga 1 kg kentang adalah a rupiah dan harga 1 kg wortel b rupiah.
Penyelesaian:
Cara I
3a + 2b = 13500 ........................... (1)
2a + b = 8500 ........................... (2)
Ubahlah sistem persamaan ke bentuk persamaan matriks.
${\begin{bmatrix} 3&2\\ 2&1 \end{bmatrix}}$ = $\begin{bmatrix} 13.500 \\ 8.500 \end{bmatrix}$
maka untuk menentukan nilai x dan y dengan rumus Metode Determinan Matriks:
nilai x = $\frac{{\begin{bmatrix} 13500&2\\ 8500&1 \end{bmatrix}}}{{\begin{bmatrix} 3&2\\ 2&1 \end{bmatrix}}}$ = $\frac{13500.1 - 2.8500}{3.1 - 2.2}$ = $\frac{13500 - 17000}{3 - 4}$ = 3500
nilai y = $\frac{{\begin{bmatrix} 3&13500\\ 2&8500 \end{bmatrix}}}{{\begin{bmatrix} 3&2\\ 2&1 \end{bmatrix}}}$ = $\frac{3.8500 - 2.13500}{3.1 - 2.2}$ = $\frac{25500 - 27000}{3 - 4}$ = 1500
Cara II
3a + 2b = 13500 ........................... (1)
2a + b = 8500 ........................... (2)
Ubahlah sistem persamaan ke bentuk persamaan matriks.
${\begin{bmatrix} 3&2\\ 2&1 \end{bmatrix}}$ = $\begin{bmatrix} 13.500 \\ 8.500 \end{bmatrix}$
maka untuk menentukan nilai x dan y dengan rumus Metode Invers Matriks:
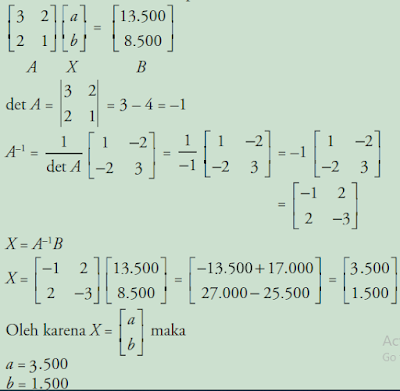

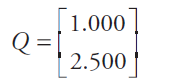
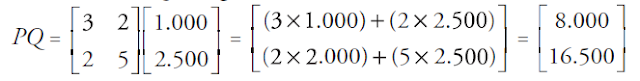
Post a Comment for "Penerapan Matriks Pada Sistem Persemaan Linear Dua Variabel"