Persamaan Garis Singgung Lingkaran
hello teman-teman materi kali ini kita akan membahas mengenai persamaan garis singgung lingkaran yaitu: menentukan persamaan lingkaran dengan titik singgung yang memiliki persamaan garis singgung lingkaran. sebelumnya kita sudah membahas mengenai kedudukan dua buah lingkaran, persamaan lingkaran yaitu bagaimana cara menentukan jari-jari pada persamaan lingkaran, cara menentukan titik pusat pada persamaan lingkaran, dan menentukan jarak antara kedua titik pada bidang koordinat.
Daftar Isi
Persamaan Lingkaran x^{2} + y^{2} = r^{2} dengan titik singgung (p,q) memiliki persamaan garis singgung lingkaran px + qy = r^{2}
perhatikan gambar dibawah ini:
keterangan:
di gambar diatas terdapat 1 buah lingkaran yang berbentuk x^{2} +
y^{2} = r^{2} dan garis lurus px + qy = r^{2} yang saling bersinggungan
pada satu titik yaitu (p,q) untuk lebih jelasnya perhatikan contoh soal
berikut:
contoh soal 1
gambarkanlah dan tentukan persamaan garis singgung
lingkaran x^{2} + y^{2} = 18 di titik singgung
(3,3)
penyelesaian:
p = 3
q = 3
r^{2} = 18
rumus persamaan garis singgung lingkaran: px + qy =
r^{2}
3x + 3y = 18 .... kedua ruas dibagi 3
x + y = 6
maka grafiknya:
contoh soal 2
gambarkanlah dan tentukan
persamaan garis singgung
lingkaran x^{2} + y^{2}
= 26 di titik singgung (5,1)
penyelesaian:
p = 5
q = 1
r^{2} = 26
rumus persamaan garis
singgung lingkaran: px + qy
= r^{2}
5x + y = 26
jadi, persamaan garis
singgung lingkaran adalah 5x
+ y = 26
maka grafiknya:
contoh
soal 3:
gambarkanlah
dan
tentukan
persamaan
garis
singgung
lingkaran
x^{2}
+
y^{2}
= 10
di
titik
singgung
(-3,1)
penyelesaian:
p =
-3
q =
1
r^{2}
= 10
rumus
persamaan
garis
singgung
lingkaran:
px +
qy =
r^{2}
-3x
+ y
=
10
jadi,
persamaan
garis
singgung
lingkaran
adalah
-3x
+ y
= 10
maka
grafiknya:
contoh
soal
4:
gambarkanlah
dan
tentukan
persamaan
garis
singgung
lingkaran
x^{2}
+
y^{2}
=
18
di
titik
singgung
(3,-3)
penyelesaian:
p
=
3
q
=
-3
r^{2}
=
18
rumus
persamaan
garis
singgung
lingkaran:
px
+
qy
=
r^{2}
3x
-
3y
=
18
x
-
y
=
6
jadi,
persamaan
garis
singgung
lingkaran
adalah
x
-
y
=
6
maka
grafiknya:
Persamaan Lingkaran (x-a)^{2} + (y-b)^{2} = r^{2} dengan titik singgung (p,q) memiliki persamaan garis singgung lingkaran (p-a)(x-a) + (q-b)(y-b) = r^{2}
perhatikan
gambar
dibawah
ini:
keterangan:
di
gambar
diatas
terdapat
1
buah
lingkaran
yang
persamaannya
(x-a)^{2}
+
(y-b)^{2}
=
r^{2}
dan
garis
lurus
(p-a)(x-a)
+
(q-b)(y-b)
=
r^{2}
yang
saling
bersinggungan
pada
satu
titik
yaitu
(p,q)
untuk
lebih
jelasnya
perhatikan
contoh
soal
berikut:
contoh
soal
1
gambarkan
dan
tentukan
persamaan
garis
singgung
Lingkaran
(x+6)^{2}
+
(y-6)^{2}
=
40
dengan
titik
singgung
(0,8).
penyelesaian:
a
=
-6
b
=
6
p
=
0
q
=
8
r^{2}
=
40
rumus
persamaan
garis
singgung
lingkaran:
(p-a)(x-a)
+
(q-b)(y-b)
=
r^{2}
(0-(-6))(x-(-6))
+
(8-6)(y-6)
=
40
(0
+
6)
(x
+
6)
+
2(y-6)
=
40
6(x+6)
+
2y
-
12
=
40
6x
+
36
+
2y
-
12
=
40
6x
+
2y
+
24
=
40
6x
+
2y
=
40
-
24
6x
+
2y
=
16
.........kedua
ruas
dibagi
2
3x
+
y
=
8
jadi,
persamaan
garis
singgung
lingkaran
adalah
3x
+
y
=
8
maka
grafiknya:
contoh
soal
2
gambarkan
dan
tentukan
persamaan
garis
singgung
Lingkaran
(x-8)^{2}
+
(y-6)^{2}
=
32
dengan
titik
singgung
(4,10).
penyelesaian:
a
=
8
b
=
6
p
=
4
q
=
10
r^{2}
=
32
rumus
persamaan
garis
singgung
lingkaran:
(p-a)(x-a)
+
(q-b)(y-b)
=
r^{2}
(4-8)(x-8)
+
(10-6)(y-6)
=
32
(-4)
(x
-
8)
+
4(y-6)
=
32
-4x
+
32
+
4y
-
24
=
32
-4x
+
4y
+
8
=
32
-4x
+
4y
=
32
-
8
-4x
+
4y
=
24
.........kedua
ruas
dibagi
-4
x
-
y
=
-6
jadi,
persamaan
garis
singgung
lingkaran
adalah
x
-
y
=
-6
maka
grafiknya:
contoh
soal
3:
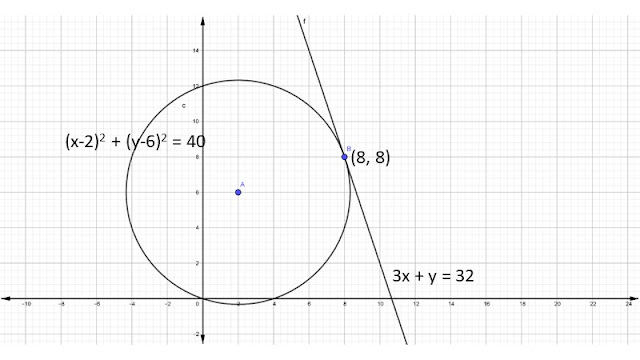
gambarkan dan tentukan persamaan garis singgung Lingkaran (x-2)^{2} + (y-6)^{2} = 40 dengan titik singgung (8,8).
penyelesaian:
a = 2
b = 6
p = 8
q = 8
r^{2} = 40
rumus persamaan garis singgung lingkaran: (p-a)(x-a) + (q-b)(y-b) = r^{2}
(8-2)(x-2) + (8-6)(y-6) = 40
(6) (x - 2) + 2(y-6) = 40
6x - 12 + 2y - 12 = 40
6x + 2y - 24 = 40
6x + 2y = 40 + 24
6x + 2y = 64
6x + 2y = 64 .........kedua ruas dibagi 2
3x + y = 32
jadi, persamaan garis singgung lingkaran adalah 3x + y = 32
maka grafiknya:
Persamaan Lingkaran x^{2} + y^{2} +Ax + By + C= 0 dengan titik singgung (p,q) memiliki persamaan garis singgung lingkaran px + qy+ \frac{1}{2}A(x+p) + \frac{1}{2}B(y+q) + C = 0
perhatikan
gambar
dibawah
ini:
keterangan:
di
gambar
diatas
terdapat persamaan lingkaran
yang
berbentuk x^{2} + y^{2} +Ax + By + C= 0
dan
garis
lurus
px + qy+ \frac{1}{2}A(x+p) + \frac{1}{2}B(y+q) + C = 0
yang
saling
bersinggungan
pada
satu
titik
yaitu
(p,q)
untuk
lebih
jelasnya
perhatikan
contoh
soal
berikut:
contoh
soal
1
gambarkan dan tentukan persamaan garis singgung Lingkaran x^{2} + y^{2} -8x -4y + 10 = 0 dengan titik singgung (7,1).
penyelesaian:
A = -8
B = -4
p = 7
q = 1
C = 10
rumus persamaan garis singgung lingkaran: px + qy+ \frac{1}{2}A(x+p) + \frac{1}{2}B(y+q) + C = 0
px + qy+ \frac{1}{2}A(x+p) + \frac{1}{2}B(y+q) + C = 0
7x + y + \frac{1}{2}(-8)(x+7) + \frac{1}{2}(-4)(y+1) + 10 = 0
7x + y + (-4)(x+7) + (-2)(y+1) + 10 = 0
7x + y -4x - 28 - 2y -2 + 10 = 0
3x -y -20 = 0
jadi, persamaan garis singgung lingkaran adalah 3x -y -20 = 0
maka grafiknya:
contoh
soal
2
gambarkan dan tentukan persamaan garis singgung Lingkaran x^{2} + y^{2} -18x -4y + 68 = 0 dengan titik singgung (5,3).
penyelesaian:
A = -18
B = -4
p = 5
q = 3
C = 68
rumus persamaan garis singgung lingkaran: px + qy+ \frac{1}{2}A(x+p) + \frac{1}{2}B(y+q) + C = 0
px + qy+ \frac{1}{2}A(x+p) + \frac{1}{2}B(y+q) + C = 0
5x + 3y + \frac{1}{2}(-18)(x+5) + \frac{1}{2}(-4)(y+3) + 68 = 0
5x + 3y + (-9)(x+5) + (-2)(y+3) + 68 = 0
5x + 3y -9x - 45 - 2y - 6 + 68 = 0
-4x + y - 51 + 68 = 0
-4x + y + 17 = 0 ....kedua ruas dikali -1
4x - y - 17 = 0
jadi, persamaan garis singgung lingkaran adalah 4x - y - 17 = 0
maka grafiknya:
contoh
soal
3:
gambarkan dan tentukan persamaan garis singgung Lingkaran x^{2} + y^{2} -2x -4y -3 = 0 dengan titik singgung (-1,4).
penyelesaian:
A = -2
B = -4
p = -1
q = 4
C = -3
rumus persamaan garis singgung lingkaran: px + qy+ \frac{1}{2}A(x+p) + \frac{1}{2}B(y+q) + C = 0
px + qy+ \frac{1}{2}A(x+p) + \frac{1}{2}B(y+q) + C = 0
-x + 4y + \frac{1}{2}(-2)(x - 1) + \frac{1}{2}(-4)(y + 4) - 3 = 0
-x + 4y + (-1)(x - 1) + (-2)(y + 4) - 3 = 0
-x + 4y -x + 1 - 2y - 8 -3 = 0
-2x + 2y + 1 - 11 = 0
-2x + 2y - 10 = 0 ....kedua ruas dibagi -2
x - y + 5 = 0
jadi, persamaan garis singgung lingkaran adalah x - y + 5 = 0
maka grafiknya:
Penutup
Demikian penjelasan tentang Persamaan Garis Singgung Lingkaran, Persamaan Garis Singgung Lingkaran merupakan bagian dari aljabar matematika mulai dari pengertian, unsur, hingga operasi hitungnya. ini penting untuk dipelajari terutama bagi siswa yang bercita-cita ingin menekuni bidang eksat atau keperguruan tinggi karena akan ada banyak materi yang menerapkan aljabar.
Post a Comment for "Persamaan Garis Singgung Lingkaran"